domingo, 30 de noviembre de 2014
sábado, 29 de noviembre de 2014
Claudio Naranjo
“LA EDUCACIÓN QUE TENEMOS ROBA A LOS JÓVENES LA CONCIENCIA, EL TIEMPO Y LA VIDA” -ENTREVISTA CON CLAUDIO NARANJO
Cuando uno escucha a este psiquiatra chileno da la sensación de estar frente al Jean-Jacques Rousseau de nuestro tiempo.
Cuenta que estaba bastante dormido hasta que en los años 60 se fue a vivir a EE.UU., allí fue discípulo de Fritz Perls, uno de los grandes terapeutas del siglo XX y formó parte del equipo del Instituto Esalen en California. Allí tuvo grandes experiencias en el mundo terapéutico y en el mundo espiritual. Contactó con el sufismo y se convirtió en uno de los introductores de Eneagrama en occidente. También bebió del budismo tibetano y el zen.
Claudio Naranjo ha dedicado su vida a la investigación y a la docencia en Universidades como Hardvard y Berkeley. Ha fundado el programa SAT, una integración de la terapia Gestalt, el Eneagrama y la Meditación para enriquecer la formación de profesores. En este momento está lanzando un aviso muy contundente: o cambiamos la educación o este mundo se va a pique.
-Dices que para cambiar el mundo hay que cambiar la educación ¿cuál es la problemática de la educación y cuál es tu propuesta?
-La problemática en la educación no es de ninguna manera la que a los educadores les parece que es. Creen que los estudiantes ya no quieren lo que se les ofrece. A la gente se le quiere forzar a una educación irrelevante y se defiende con trastornos de la atención, con desmotivación. Yo pienso que la educación no está al servicio de la evolución humana sino de la producción o más bien de la socialización. Esta educación sirve para domesticar a la gente de generación en generación para que sigan siendo unos corderitos manipulables por los medios de comunicación. Esto es socialmente un gran daño. Se quiere usar la educación como una manera de meter en la cabeza de la gente una manera de ver las cosas que le conviene al sistema, a la burocracia. Nuestra mayor necesidad es la de una educación para evolucionar, para que la gente sea lo que podría ser.
La crisis de la educación no es una crisis más entre las muchas crisis que tenemos, sino que la educación está en el centro del problema. El mundo está en una crisis profunda porque no tenemos una educación para la conciencia. Tenemos una educación que en cierto modo le está robando a la gente su conciencia, su tiempo y su vida.
El modelo de desarrollo económico de hoy ha eclipsado el desarrollo de la persona.
-¿Cómo sería una educación para que seamos seres completos?
-La educación enseña a la gente a pasar exámenes, no a pensar por si misma. En un examen no se mide la comprensión, se mide la capacidad de repetir. ¡Es ridículo, se pierde una cantidad tan grande de energía! En lugar de una educación para la información, se necesitaría una educación que se ocupe del aspecto emocional y una educación de la mente profunda. A mi me parece que estamos presos entre una alternativa idiota, que es la educación laica y una educación autoritaria que es la educación religiosa tradicional. Está bien separar Estado e Iglesia pero, por ejemplo en España, han echado por la borda el espíritu como si religión y espíritu fueran la misma cosa. Necesitamos que la educación atienda también a la mente profunda.
-¿Cuándo hablas de espiritualidad y de mente profunda a qué te refieres exactamente?
-Tiene que ver con la conciencia misma. Tiene que ver con aquella parte de la mente de la que depende el sentido de la vida. Se está educando a la gente sin ese sentido. Tampoco es la educación de valores porque la educación de valores es demasiado retórica e intelectual. Los valores deberían ser cultivados a través de un proceso de transformación de la persona y esta transformación está muy lejos de la educación actual.
La educación también tiene que incluir un aspecto terapéutico. Desarrollarse como persona no se puede separar del crecimiento emocional. Los jóvenes están muy dañados afectiva y emocionalmente por el hecho de que el mercado laboral se traga a los padres y ya no tienen disponibilidad para los hijos. Hay mucha carencia amorosa y muchos desequilibrios en los niños. No puede aprender intelectualmente una persona que está dañada emocionalmente.
Lo terapéutico tiene mucho que ver con devolverle a la persona la libertad, la espontaneidad y la capacidad de conocer sus propios deseos. El mundo civilizado es un mundo domesticado y la enseñanza y la crianza son instrumentos de esa domesticación. Tenemos una civilización enferma, los artistas se dieron cuenta hace mucho tiempo y ahora cada vez más los pensadores.
-A la educación parece solo interesarle desarrollar la parte racional de la gente ¿Qué otras cosas podrían desarrollarse?
-Yo pongo énfasis en que somos seres con tres cerebros: tenemos cabeza (cerebro intelectual), corazón (cerebro emocional) y tripas (cerebro visceral o instintivo). La civilización está íntimamente ligada por la toma de poder por el cerebro racional. Con el momento en que los hombres predominaron en el dominio político, unos 6000 años atrás, se instaura esto que llamamos civilización. Y no es solamente el dominio masculino ni el dominio de la razón sino también de la razón instrumental y práctica, que se asocia con la tecnología; es este predominio de la razón instrumental sobre el afecto y sobre la sabiduría instintiva lo que nos tiene tan empobrecidos. La plenitud la puede vivir sólo una persona que tiene sus tres cerebros en orden y coordinados. Desde mi punto de vista necesitamos una educación para seres tri-cerebrados. Una educación que se podría llamar holística o integral. Si vamos a educar a toda la persona, hemos de tener en cuenta que la persona no es solo razón.
-La educación nos sumerge en un mar de conceptos que nos separan de la realidad y nos aprisiona en nuestra propia mente ¿Cómo se puede salir de esa prisión?
-Es una gran pregunta y es una pregunta necesaria en el mundo educacional. La idea de que lo conceptual sea una prisión requiere una cierta experiencia de que la vida es más que eso. Para uno que ya tiene el interés en salir de la prisión de lo intelectual, es muy importante la disciplina de detener la mente, la disciplina del silencio, como se practica en todas las tradiciones espirituales: cristianismo, budismo, yoga, chamanismo… Parar los diálogos internos en todas las tradiciones de desarrollo humano ha sido visto como algo muy importante. La persona necesita alimentarse de otra cosa que conceptos. La educación quiere encerrar a la persona en un lugar donde se la somete a una educación conceptual forzada, como si no hubiera otra cosa en la vida. Es muy importante, por ejemplo, la belleza. La capacidad de reverencia, de asombro, de veneración, de devoción. No tiene que ver necesariamente con una religión o con un sistema de creencias. Es una parte importante de la vida interior que se está perdiendo de la misma manera en que se están perdiendo los espacios bellos de la superficie de la Tierra, a medida que se construye y se urbaniza.
-Precisamente quería preguntarte tu opinión sobre la crisis ecológica que vivimos.
-Es una crisis muy evidente, es la amenaza más tangible de todas. Se puede prever fácilmente que con el calentamiento de la Tierra, con el envenenamiento de los océanos y otros desastres que están pasando, no vamos a poder sobrevivir tantas personas como las que somos ahora.
Estamos viviendo gracias al petróleo y consumimos más recursos de los que la tierra produce. Es una cuenta atrás. Cuando se nos acabe el combustible será un desastre para el mundo tecnológico que tenemos.
La gente a la que llamamos más primitiva como los indígenas tienen una forma de tratar a la naturaleza que no viene del sentido utilitario. En la ecología como en la economía y otras cosas, hemos querido prescindir de la conciencia y funcionar sólo con argumentos racionales y eso nos está llevando al desastre. La crisis ecológica sólo puede pararse con un cambio de corazón, verdadera transformación, que sólo la puede dar un proceso educativo. Por eso no tengo mucha fe ni en las terapias ni en las religiones. Solo una educación holística podría prevenir el deterioro de la mente y del planeta.
-¿Podríamos decir que has encontrado un equilibrio en tu vida a esas alturas?
-Yo diría que cada vez más, aunque no he terminado el viaje. Soy una persona que tiene mucha satisfacción, la satisfacción de estar ayudando al mundo en el que estoy. Vivo feliz, si se puede ser feliz en esa situación trágica en la que estamos todos.
-Desde tu experiencia, tu trayectoria y tu madurez, ¿cómo procesas el hecho de la muerte?
-En todas las tradiciones espirituales se aconseja vivir con la muerte al lado. Hay que hacerse a esa evidencia de que somos mortales y creo que el que toma la muerte en serio no será tan vano. No tienes tanto miedo a cosas pequeñas cuando hay una cosa grande de la cual preocuparte más. Yo creo que la muerte sólo puede superarla uno que en cierto modo muere antes de morir. Uno tiene que morir a la parte mortal, a la parte intrascendente. Los que tienen suficiente tiempo y vocación y que llegan suficientemente lejos en este viaje interior se encuentran tarde o temprano con su verdadero ser. Y ese ser interior o ese ser lo que uno es, es algo que no tiene tiempo y que le da a una persona una cierta paz o un sentido de invulnerabilidad. Estamos muy absortos en nuestra vida cotidiana, en nuestros pensamientos de alegría, tristeza, etc… No estamos en nosotros, no estamos atentos a quien somos. Para eso necesitamos estar muy en sintonía a nuestra experiencia del momento. Esta es la condición humana, estamos viviendo hacia el pasado y el futuro, el aspecto horizontal de nuestra vida. Pero poco atentos a la dimensión vertical de nuestra vida, el aspecto más alto y más profundo, eso es el espíritu y es nuestro ser y la llave para acceder es el aquí y ahora.
A veces vamos en busca del ser y a veces nos confundimos en la búsqueda de otras cosas menos importantes como la gloria.
Garabatos de Euler
El garabato de Euler
 Leonardo era un niño inteligente y soñador. Le gustaba mucho el cine, las matemáticas y los inventos. Le encantaba su nombre, Leonardo, pues era también el nombre de Leonardo Da Vinci y de Leonhard Euler, sabios entre sabios. Aunque muchas personas le decían, - "Ah, Leonardo, como Leonardo Di Caprio".
Leonardo era un niño inteligente y soñador. Le gustaba mucho el cine, las matemáticas y los inventos. Le encantaba su nombre, Leonardo, pues era también el nombre de Leonardo Da Vinci y de Leonhard Euler, sabios entre sabios. Aunque muchas personas le decían, - "Ah, Leonardo, como Leonardo Di Caprio". |
| Garabato de Euler Vértices + Caras = Aristas + 2 10 + 11 = 19 + 2 |
Moraleja: ni todos los niños son iguales ni todos los garabatos son insignificantes.
La característica de Euler en los poliedros regulares
 |
| Poliedros regulares Imágen de tierno2ba.blogspot.com.es |
Esta fórmula se cumple también en todos los poliedros convexos. Pero también puedes realizar el siguiente ejercicio:
- Dibuja un garabato sin levantar el lápiz del papel y termina en el mismo lugar en el que lo comenzaste.
- Dibuja vértices en los puntos en los que la líneas se cruzan.
- Cuenta Aristas, Zonas y Vértices y comprueba como la fórmula o característica de Euler se cumple.
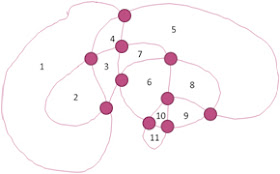 |
| Garabato de Euler Vértices + Caras = Aristas + 2 10 + 11 = 19 + 2 |
Belleza en mates
¿Pueden las precisas y hermosas melodías de las "Las bodas de Fígaro", de Mozart, tener la misma impresión de belleza en el cerebro que la fórmula matemática de la teoría de la relatividad de Albert Einstein?
Parece que sí. Una investigación realizada por científicos de la Universidad de Londres reveló que una compleja cadena de números y letras en una fórmula matemática puede evocar las mismas sensaciones de belleza que una obra maestra de la música.
El estudio consistió en ubicar delante de matemáticos lo que eran consideradas ecuaciones "feas" y "bellas" y allí se pudo observar, mediante el uso de escáner conectado al cerebro, que al mirar las ecuaciones consideradas sublimes tenían la misma reacción neuronal que al apreciar una obra de arte.
Los investigadores sugirieron, basados en estos datos, que es posible que exista una base neurobiológica de la belleza.
Todo esto porque raramente se expresa de igual manera el gusto por la fórmula de la identidad de Euler o el teorema de Pitágoras como se hace cuando se escucha lo mejor de Beethoven o se observa un cuadro de Van Gogh.
Lea: Cómo componer música con ondas cerebrales
Fórmulas estéticas
Para realizar el estudio, publicado en la publicación académica Frontier, se le entregaron a 15 matemáticos 60 fórmulas para calificar su estética.
"Un gran número de áreas del cerebro están involucradas cuando observas una ecuación matemática, pero cuándo les pides que las califiquen por su belleza, la parte emocional del cerebro se activa, como si estuvieras viendo una pintura", le dijo a la BBC el profesor Semir Zeki, que formó parte de la investigación.
Entre más bella calificaban la fórmula, más actividad era registrada en las imágenes de resonancia magnética (MRI, por sus siglas en inglés) que se tomaban en esos momentos.
"La neurociencia no puede afirmar que tan bello es algo, pero si se logra involucrar la parte medio orbito-frontal del cerebro, como sucede con los matemáticos y las ecuaciones, se puede encontrar belleza en todo", afirmó Zeki.
La identidad de Euler
A simple vista tal vez la fórmula de la identidad de Euler no sea muy "linda" o "artística", pero en el estudio fue la mejor calificada por los académicos.
Para el profesor David Percy, del Instituto de Aplicaciones de la Matemática de Reino Unido, ésa es su favorita.
"Es un verdadero clásico y es posible que no se pueda hacer algo mejor que eso", dijo Percy.
Y añadió que "combina de manera increíble las constantes más importantes de la matemática: cero (identidad aditiva), uno (identidad multiplicadora), e ypi (los números transcendentales más comunes) y el último que es i (el número imaginario)".
Para Percy lo que hay que tener claro es que el impacto al observar estas ecuaciones no es inmediato, sino gradual. Como con una composición musical, que después de escucharla varias veces es que se puede apreciar su potencial real.
"Su estética ha sido fuente de inspiración y te da el entusiasmo para encontrar cosas nuevas", concluyó Percy.
Belleza innegable
Para el matemático Marcus Du Sautoy es innegable la belleza de las matemáticas y que eso es lo que inspira a cada uno de los matemáticos en su trabajo.
"Amo las cosas que Pierre de Fermat hizo. Él demostró que cualquier número primo que se puede dividir por cuatro y sobra uno, fue la suma de dos números cuadrados", señaló Du Sautoy.
Por supuesto, puso un ejemplo: "Veamos, 41 es un número primo que al dividirlo por cuatro y sobra uno, es igual a la suma de 25 (cuadrado de cinco) más 16 (cuadrado de cuatro). Lo que nos recuerda que es una cifra que se puede escribir en dos números cuadrados".
Du Sautoy aclaró que es inesperado que en matemáticas estas dos cosas (números primos y cuadrados) tengan algo en común, pero sirve como prueba de cómo dos ideas separadas se van mezclando al igual que en una composición musical las notas se van juntando.
"Pero lo placentero es el camino que recorres para estudiarlo o para crearlo, como en un cuadro o una composición, no basta con la interpretación o la exposición en un museo", concluyó.
En el estudio, los matemáticos calificaron la serie infinita de Srinivasa Ramanujan y la ecuación funcional de Bernhard Riemann como las más "feas".
viernes, 28 de noviembre de 2014
Intuiciones para una clase .... - 7mo.
2) Limpiar la pizarra.
3) Poner Fecha.
4) Poner el Eje Temático: Geometría.
5) Dejar un espacio para poner el AE de la clase:
(No llenarlo, para generar una inquietud inicial)
6) Magia: ¡ Bomba de DADOS !
(Materiales: Magia de la Bomba de Dados)
7) Explicar la Metáfora.
8) Iniciar Variaciones de elementos Lineales, dividiendo la pizarra en ANTES y DESPUES y comprar lo que sucede al dobla una longitud con
a) Perímetro ;
b) Área ;
c) Volumen.
El ejemplo más simple, que hace el profesor con ayuda de los chicos y chicas:
(Nota: Se puede organizar de otra forma, como en una película, con un antes y un después)
REDONDEAR el sentido de del proceso iniciado en Aula.
AE 10:
Formular y verificar conjeturas, en casos particulares, relativas a cambios en el perímetro de polígonos al variar uno o más de sus elementos lineales.
AE 11:
Formular y verificar conjeturas, en casos particulares, relativas a cambios en el volumen de prismas rectos y pirámides al variar uno o más de sus elementos lineales.
martes, 25 de noviembre de 2014
domingo, 23 de noviembre de 2014
Lynn Margulis
sábado, 22 de noviembre de 2014
Animaciones y matematicas
Si uno piensa en los magos de Pixar quizá se le vengan a la cabeza sus inagotables directores o la magia que sacan de actores de sobra conocidos. O los guionistas que han elaborado esas fábulas engañosamente simples por las que no pasa el tiempo; ahí está la trlogía de Toy story como prueba. O incluso los diseñadores que han logrado que un viejo huraño como el Up acabe cayendo simpático, que el montón de metal sin capacidad de habla de Wall-E emocionara como si lo hubiera parido E.T. Pero muy poca gente piensa en los matemáticos.
En realidad, el verdadero secreto de esa magia aparentemente intangible de la casa no está en las artes, sino en las ciencias. Sin la matemática pura y dura, muchas de las historias no se hubieran contado como las conocemos ahora. Un nuevo vídeo, protagonizado por el físico clave en Pixar Tony DeRose en el portal matemático Numberphile, lo revela. La clave no está en los unos y ceros de los ordenadores de la compañía, sino en la geometría. En los millones de diminutas formas que, gracias al arte de DeRose, se esconden bajo la piel de los personajes y que son lo que les da personalidad.
Para entenderlo basta con ver el vídeo en el minuto 1:30: DeRose convierte un robo en una superficie suave. En el minuto 2:45 se ve el mismo proceso en 3-D y en el 3:17, el uso que tiene en el cine. Si el proceso suena excesivamente simple –el propio presentador lo dice–, pueden someterse a la explicación que empieza en el minuto cinco con todos los números. Todo obedece a un sentido estético cimentado en los números que dictan las proporciones de cada microscópica forma.
Si no pueden ver el vídeo, DeRose explica su técnica con un rombo. Su método crea puntos medios en las aristas del polígono y luego desplaza todos los puntos a la mitad de distancia del punto vecino, convirtiendo el rombo en un hexágono irregular. Repite este proceso las veces que crea necesario hasta lograr la suavidad que busca, asemejándo la forma cada vez más a un círculo. Esto es lo que hace, con una mayor complejidad, con los modelos en tres dimensiones que crean los animadores hasta darles el aspecto deseado.
¿Y por qué es todo esto tan especial? Tony DeRose, licenciado en Física y doctorado en Ciencia Computacional por la universidad de California, es uno de las más respetadas mentes matemáticas de Pixar. TIene en su haber decenas de artículos científicos. Profesor de 1986 a 1995 en la universidad de Washington, sus escritos tocan siempre el mismo tema, el campo de los gráficos generados por ordenador. No es casualidad que, tras dejar la academia, se uniera a la división de mentes matemáticas de Pixar, donde su primera gran aportación le valió un Oscar con Geri's Game, un corto de un anciano que se reta a sí mismo al ajedrez.
Y esta técnica que explica –por cierto, en el edificio bautizado con el nombre del benefactor económico de la empresa, Steve Jobs–, es la que le ha dado la fama, recopilada en un texto titulado Subdivision Surfaces in Character Animation. El texto es un clásico del mundillo y tiene su origen en el momento en el que DeRose llega al mundo de la animación: la forma más habitual de modelar superficies complejas y suaves era usando NURBS, un modelo matemático que calcula superficies curvas a partir de polígonos.
Pero, según explica el artículo de DeRose, este modelo presentaba algunos problemas. Era caro de realizar, tendía a presentar fallos en las cifras y, al animarlos, esa suavidad necesaria desaparecía. El autor ponía como ejemplo todo el trabajo manual que se requirió en Toy Storypara esconder este defecto en la cara del protagonista.
Ahí es donde entra su técnica. “La experiencia es extremadamente positiva”, avisa en su artículo, añadiendo que dota a los modeladores una libertad que con NURBS no tenían, “lo que reduce dramáticamente el tiempo que deben dedicar a crear y planear un modelo inicial” y facilitando su trabajo. DeRose lidera hoy la división de investigación de Pixar, que emplea a once personas, principalmente científicos computacionales.
Pixar se alimenta de la pasión entre el matrimonio entre la ciencia y el arte. Sus orígenes se remontan a 1979, cuando George Lucas, tras el taquillazo de La Guerra de las Galaxias, contrató a Ed Catmull, un científico loco por la animación, para su división de gráficos por ordenador. Tras años dedicándose a desarrollar las técnicas de efectos especiales generados por ordenador para LucasFilm, Catmull decidióindependizarse y fundar Pixar junto con 38 compañeros de trabajo, con Steve Jobs como principal inversor.
Doctorado también en Ciencia Computacional, Catmull es un pionero en su campo, creador de varias técnicas de animación, como el efecto de profundidad conocido como z-buffer, y programas como el Renderman, con el que se hicieron los efectos de Titanic o del precuelas de La Guerra de las Galaxias. Las ecuaciones que la técnica de DeRose usa para formas complejas fueron desarrolladas por Catmull y su compañero Clark hace ya 40 años. Su segundo de a bordo fue Alvy Ray Smith, otro de esos genios de la animación con un doctorado en Ciencias Computacionales, profesor en Berkeley hasta 1974 y que acabó trabajando para Microsoft tras varios desacuerdos con el fundador de Apple.
Con este bagaje no es de extrañar que Pixar tenga, desde sus inicios, esa división científica. De ella salen cada año numerosos artículos sobre animación con nombres tan sugerentes como Simulación artística del cabello rizado, que explica la creación del motor gráfico que animó el pelo de la protagonista de Brave, o Todo el mundo puede cocinar, dentro de la cocina de Ratatouille. Hay otros con títulos tan soporíferos comoProblemas avanzados en el nivel de detalle o Mapeado de texturas para un mejor modelo dipolar. La cuestión es que tanto los artículos divertidos como los aburridos son los que hacen posible que los personajes de Pixar triunfen como resultado del amor entre la ciencia y el arte.
Extraña vida .... Un matemático y político a la vez ....
Alexandre Grothendieck, un genio de las matemáticas recompensado con el premio Fields y conocido por sus firmes posiciones pacifistas y ecologistas, falleció a los 86 años tras haber vivido las dos últimas décadas como un ermitaño en un pueblo de los Pirineos.
Grothendieck, apátrida hasta que en 1971 aceptó la nacionalidad francesa, falleció ayer en el hospital de Saint-Girons, en la cordillera pirenaica que separa Francia y España, donde había vivido aislado del mundo desde 1990, informaron hoy fuentes cercanas al científico.
Desconocido para el gran público y considerado por muchos de sus colegas uno de los matemáticos más importantes del siglo XX, Grothendieck (Berlín, 1928) era hijo de una periodista socialista revolucionaria y de un fotógrafo anarquista judío ruso que emigró a Alemania tras haber sido condenado primero por el régimen zarista y luego por los comunistas.
Sus padres tuvieron también que abandonar Alemania tras el ascenso de los nazis al poder y partieron a Francia, antes de poner rumbo a España para sumarse a la causa republicana.
El pequeño Alexandre quedó al cuidado de un amigo de la familia en Hamburgo hasta que la familia volvió a reunirse en Nîmes al término de la guerra civil española, en 1939, pero los Grothendieck pasaron poco tiempo juntos.
Meses después, el padre fue enviado a Auschwitz, donde muere en 1942. La madre y el pequeño terminaron en el campo de concentración de Rieucros, en los Pirineos, donde Alexandre comenzó a interesarse por las matemáticas.
Sin un expediente brillante, acabó el colegio y estudió matemáticas en Montpellier, donde un profesor detectó en el joven licenciado ciertas aptitudes extraordinarias.
Pero el mito sobre su genialidad no se forjó hasta que los grandes matemáticos Laurent Schwartz y Jean Dieudonné le entregaron, cuando tenía 20 años, una lista con catorce problemas sobre los que trabajar en los próximos años y le pidieron que eligiera uno.
Unos meses más tarde, Alexandre Grothendieck regresó a ver a sus maestros con los catorce problemas resueltos.
En los meses posteriores redactó el equivalente a seis tesis, trabajo que a un alumno aplicado le habría llevado entre tres y cuatro años.
Los años siguientes, el joven prodigio se dedicó al análisis funcional, un trabajo revolucionario pero menos trascendente que sus estudios posteriores, donde destacó por su capacidad para generalizar y generar nuevos puntos de vista.
Con el pasaporte Nansen que la ONU otorgaba a los refugiados sin patria ya que rechazaba asumir la nacionalidad francesa, Grothendieck trabajó a partir de 1953 durante dos años como profesor en Brasil y Estados Unidos, antes de enrolarse en el Instituto de Altos Estudios Científicos (IHES), al sur de París y financiado por el empresario Léon Motchane.
Fue en esa institución donde dirigió un seminario de geometría algebraica con una nueva visión sobre la geometría inspirada en su obsesión por repensar el espacio con nociones sobre las que todavía hoy trabajan los matemáticos.
En 1966 recibió la medalla Fields, considerada el Nobel de las matemáticas, un premio que no fue a recoger por motivos políticos y que después subastó para financiar a los norvietnamitas en la guerra contra Estados Unidos.
No fue el único galardón -y dotaciones económicas- que rechazó Grothendieck, quien opinaba que sus trabajos debería juzgarlos el tiempo y no los hombres, y que paulatinamente fue alejándose de la comunidad científica y acercándose a movimientos ecologistas radicales.
En esos años rehusó también su puesto en el prestigioso Colegio de Francia para convertirse en profesor de la Universidad de Montpellier y, entre 1984 y 1988, en el Centro Nacional de Investigaciones Científicas de Francia (CNRS).
En 1990 se retiró a los Pirineos sin revelar donde viviría y exigió que sus escritos no publicados fueran destruidos.
Además de un matemático extraordinario, Grothendieck fue también "una personalidad fuera de lo común en su filosofía de vida", según dijo el presidente de Francia, François Hollande, en homenaje al difunto y extraño genio.
viernes, 21 de noviembre de 2014
Margaritas y Fibonacci
Me quiere… no me quiere… me quiere…
Publicado: 21 noviembre, 2014 en curiosidades, númerosEtiquetas:enamorados, Fibonacci, margaritas, matemáticas, me quiere, sucesión de Fibonacci





















