Mostrando entradas con la etiqueta Conjuntos Numéricos. Mostrar todas las entradas
Mostrando entradas con la etiqueta Conjuntos Numéricos. Mostrar todas las entradas
miércoles, 13 de julio de 2016
martes, 8 de marzo de 2016
domingo, 31 de mayo de 2015
domingo, 15 de marzo de 2015
10 puntos para entender los números Reales ( IR ) - 2do. Medio - Escuela Francisco Varela
INFINITOS por todas partes ....
por Claudio Escobar Cáceres
Departamento de Matemáticas
Escuela Francisco Varela
0)
Los matemáticos distinguen varios tipos de números, con propiedades diferentes. Lo que realmente importa no son los números individuales, sino el sistema al que pertenecen: la compañía en la que están.
Algunos de estos sistemas o conjuntos numéricos son:
IN: Naturales.
Los números de contar, esos que "vemos en la naturaleza"
IN = {1,2,3,4,5,.....}
Son infinitos, tienen un primer número, pero no un final.
- - - - - - - - - -
INo: Cardinales.
Son los Naturales agregados del cero.
INo = {0,1,2,3,4,5, .....}
Son también infinitos, tienen un primer número, pero tampoco un final.
Este conjunto numérico, contiene al anterior.
- - - - - - - - - -
Z: Enteros.
Son los naturales, más los naturales con signo negativo, más el cero.
Z = { .... -5, -4, -3, -2, -1, 0, 1, 2, 3, .... }
Son infinitos, no tienen principio ni fin.
Z contiene a IN, Z contiene a INo
- - - - - - - - - -
Q: Racionales.
(acá hay fracciones y decimales, aunque NO todos los decimales, porque algunos decimales son de otro tipo: Irracionales)
Q contiene todas las fracciones, positivas y negativas. También contiene a todos los enteros, porque cada entero se puede poner como fracción, simplemente dividiendo por 1.
Q = { .... -5, -9/2, -4, -3, -2, -3/2, -1, -1/3, 0, 1, 2/3, 2, 3, 4, 5, 11/2, .... }
Nuevamente Q contiene a Z, Q contiene a INo, Q contiene a IN.
Hasta acá conocemos, por lo general, hasta 1ro. medio.
Pero aparece otro Conjunto, los Irracionales .... Los irracionales NO contienen a ninguno de los anteriores conjuntos ....
Los racionales unidos a los irracionales conforman un conjunto mayor llamado Los Reales.
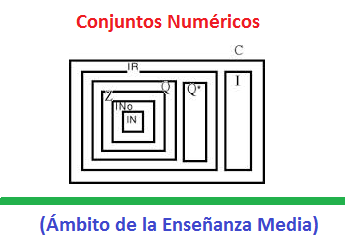
Veamos esto en un esquema:
Pero OJO Piojo:
============
IR contiene a Q
IR contiene a Q*
IR contiene a Z
IR contiene a INo
IR contiene a IN
Q* NO contiene a ninguno de los otros Conjuntos Numéricos!
Y como diagramas de Venn, pero en Brasileiro, ja ja ja !!!!
1)
Los números Reales ( IR ), están formados por la unión de dos conjuntos: Los Racionales ( Q ) y los Irracionales ( Q* ).
es decir,
Q: Racionales:
Son aquellos que se pueden escribir como fracción. Incluye a los decimales finitos, los periódicos y los semiperiódicos.
ejemplos:
2,3 (Finito) ;
-3,185 (Otro Finito) ;
0,33333..... (Periódico) ;
-5/8 ;
0,6666.....(Otro periódico) ;
-1/3 ;
2,7891212121212.... (Semiperiódico) ....
Q*: Irracionales:
Son aquellos que NO se pueden escribir como fracción, poseen un desarrollo decimal infinito en el cuál jamás se repite algún tipo de período.
ejemplos:
Al conjunto de los Reales se le conoce también como "El Continuo" ....
Nota:
Toda fracción puede escribirse como decimal, PERO
NO TODO decimal puede escribirse como fracción.
2)
Los números Reales, dijimos, se forman por la unión de los Racionales (Q) y los Irracionales (Q*).
La sola presencia de los Racionales (Q), deja incompleta la Recta Numérica, es decir, si en una recta numérica graficamos Q, que contiene como subconjuntos a IN, INo y Z, la recta estaría llena de hoyos o agujeros .... faltarían infinitos números: Faltarían los Irracionales !!!!
3)
Hasta IN, INo, Z y Q, los conjuntos numéricos se llaman ENUMERABLES, porque se pueden hacer corresponder biunívocamente (uno a uno) con los números Naturales (IN) o de contar.
De allí en adelante, es decir, Tanto los Irracionales (Q*), como los Reales ( IR), hablamos de Conjuntos Numéricos NO Enumerables, porque no se pueden hacer corresponder biunívocamente con los Naturales ( IN ).
Esto lo descubrió o al menos lo demostró Cantor.
4)
George Cantor (1845 - 1918): Matemático alemán, de origen ruso, creador de la Teoría Axiomática de Conjuntos, y el primero capaz de expresar formalmente en lenguaje matemático la idea o noción de INFINITO, bajo la forma de un nuevo conjunto numérico, los números Transfinitos.
Las ideas de Cantor acerca del infinito recibieron una crítica generalizada que tal vez agravó su tendencia crónica a la depresión, lo que a su vez le llevó muchas veces a estar internado. Sin embargo su obra se hizo trascendente y fundamental para las matemáticas actuales.
El matemático David Hilbert describió el trabajo de Cantor como "el producto más depurado de genio matemático y uno de los mayores logros de la actividad intelectual pura".
5)
Los números Racionales (Q) son infinitos y también lo son los Reales (R); sin embargo, hay más números Reales que Racionales. Georg Cantor, matemático del siglo XIX, fue el pionero en investigar esta aparente paradoja, remeciendo las bases de la matemática que se conocía al momento: al afirmar que existen distintos tipos de infinitos: algunos mayores que otros.
6)
Entre los años 1870 y 1880 Cantor y Dedekind iban a operar un cambio REVOLUCIONARIO.
De aquello que se había siempre pensado una imposibilidad: que la parte sea igual al todo, ellos hicieron una propiedad.
Ellos mostraron utilizando la correspondencia biunívoca, que el conjunto de los naturales ( IN: Números de contar ) es tan grande como los pares, por ejemplo, porque se puede hacer una correspondencia biunívoca entre los Naturales y los Pares (o impares).
El Conjunto de los Naturales ya no es mayor que el conjunto de los Pares, o de los Impares.
A este conjunto enumerado (hecho corresponder numéricamente con los naturales) se le llama Infinito Numerable o Enumerable o a veces Infinito Discreto.
De igual forma demostró Cantor que hay tabtos Naturales como Enteros (Z) y Racionales (Q).
En la imagen, una intervención artística personal a la obra de Max Ernst.
7)
¿Es el numerable el único infinito?
Cantor responde que NO.
La potencia de los números Reales es mayor que el numerable.
En efecto es imposible construir una correspondencia biunívoca entre IN y R.
Es decir, hay infinitamente más puntos en la Recta Numérica que números Naturales (o Cardinales o Enteros, o Racionales).
Tenemos dos Infinitos:
1) El numerable ( IN; INo; Z; Q)
2) el de IR, denominado "El Continuo".
Pero cuidado, de nuevo, por más asombro que le cause: No hay más puntos en todo IR, que en el segmento [0,1].
8)
Cantor dice que SÍ, que hay otros infinitos más grandes .... Dice que el conjunto de las partes de un conjunto A, tiene una potencia superior.
El conjunto de todos los subconjunto de IR, posee una INFINITUD MAYOR ....
Podemos partir de IN, luego seguir con Z, Q, Q* y construir sus conjuntos de subconjuntos ....
Hay una infinidad de infinitos.
9)
Dos tipos de Infinitos:
Así:
IN: Naturales: Alfa Cero (Infinito Numerable)
INo: Cardinales: Alfa Cero (Infinito Numerable)
Z: Enteros: Alfa Cero (Infinito Numerable)
Q: Racionales: Alfa Cero (Infinito Numerable)
------------------------------------------------------------
Q*: Irracionales: Alfa 1 (Infinito No Numerable)
IR: Reales: Alfa 1 (Infinito No Numerable)
10)
El infinito que a mi me gusta ....
Katsushika Hokusai, uno de los artistas japoneses más conocidos a nivel mundial, realizó cerca de treinta mil obras de arte a lo largo de su carrera. Aunque su estilo dista mucho del arte tradicional japonés, su obra es clave en las historia de la producción artística de este país.
Hokusai nació en 1760, en el seno de una familia de artesanos en la provincia japonesa de Edo. Comenzó a pintar desde que tenía seis años, muy probablemente bajo la tutela de su padre, cuyo trabajo era hacer espejos y decorar los marcos con meticulosas ornamentas. En 1779 publicó sus primeras piezas de ukiyo-e –estampas japonesas que mostraban distintas costumbres– como parte de una serie de impresos sobre teatro Kabuki. Durante su primera etapa creativa su estilo se regía por la tradición japonesa, tanto en técnica como en temática, pero a finales del siglo XVIII adquirió varios grabados calcográficos en cobre hechos en Francia y Holanda, que lo llevaron a explorar con diferentes estilos de Occidente. Esto influyó en los temas que trataba en sus obras, se alejó de los actores Kabuki y los cortesanos para enfocarse en el paisaje y en imágenes cotidianas de la vida en Japón, un cambio fundamental tanto para el artistas como para el género ukiyo-e.
La obra más famosa de Hokusai es Treinta y seis vistas del Monte Fuji, una serie de 36 xilografías realizadas entre 1831 y 1833. En una segunda publicación se añadieron diez xilografías más a la serie en las que el artista japonés retrata al Monte Fuji desde diferentes perspectivas y en distintas condiciones climáticas.
La gran ola de Kanagawa, también conocida como La gran ola, es la pieza más reconocida de la serie y de la carrera de Hokusai. De ésta se realizaron miles de copias, y varias llegaron a manos de coleccionistas europeos. A partir de la década de 1870, La gran ola se volvió muy popular entre artistas y coleccionistas franceses.
por Claudio Escobar Cáceres
Departamento de Matemáticas
Escuela Francisco Varela
en construcción .....
"Dios creó los números,
el resto es obra del ser humano"
(Leopold Kronecker)
0)
Los matemáticos distinguen varios tipos de números, con propiedades diferentes. Lo que realmente importa no son los números individuales, sino el sistema al que pertenecen: la compañía en la que están.
Algunos de estos sistemas o conjuntos numéricos son:
IN: Naturales.
Los números de contar, esos que "vemos en la naturaleza"
IN = {1,2,3,4,5,.....}
Son infinitos, tienen un primer número, pero no un final.
- - - - - - - - - -
INo: Cardinales.
Son los Naturales agregados del cero.
INo = {0,1,2,3,4,5, .....}
Son también infinitos, tienen un primer número, pero tampoco un final.
Este conjunto numérico, contiene al anterior.
- - - - - - - - - -
Z: Enteros.
Son los naturales, más los naturales con signo negativo, más el cero.
Z = { .... -5, -4, -3, -2, -1, 0, 1, 2, 3, .... }
Son infinitos, no tienen principio ni fin.
Z contiene a IN, Z contiene a INo
- - - - - - - - - -
Q: Racionales.
(acá hay fracciones y decimales, aunque NO todos los decimales, porque algunos decimales son de otro tipo: Irracionales)
Q contiene todas las fracciones, positivas y negativas. También contiene a todos los enteros, porque cada entero se puede poner como fracción, simplemente dividiendo por 1.
0 = 0/1
7 = 7/1
-893 = -893/1
Q = { .... -5, -9/2, -4, -3, -2, -3/2, -1, -1/3, 0, 1, 2/3, 2, 3, 4, 5, 11/2, .... }
Nuevamente Q contiene a Z, Q contiene a INo, Q contiene a IN.
Hasta acá conocemos, por lo general, hasta 1ro. medio.
Pero aparece otro Conjunto, los Irracionales .... Los irracionales NO contienen a ninguno de los anteriores conjuntos ....
Los racionales unidos a los irracionales conforman un conjunto mayor llamado Los Reales.
Veamos esto en un esquema:
============
IR contiene a Q
IR contiene a Q*
IR contiene a Z
IR contiene a INo
IR contiene a IN
Q* NO contiene a ninguno de los otros Conjuntos Numéricos!
Y como diagramas de Venn, pero en Brasileiro, ja ja ja !!!!
1)
Los números Reales ( IR ), están formados por la unión de dos conjuntos: Los Racionales ( Q ) y los Irracionales ( Q* ).
es decir,
IR = Q U Q*.
Q: Racionales:
Son aquellos que se pueden escribir como fracción. Incluye a los decimales finitos, los periódicos y los semiperiódicos.
ejemplos:
2,3 (Finito) ;
-3,185 (Otro Finito) ;
0,33333..... (Periódico) ;
-5/8 ;
0,6666.....(Otro periódico) ;
-1/3 ;
2,7891212121212.... (Semiperiódico) ....
Q*: Irracionales:
Son aquellos que NO se pueden escribir como fracción, poseen un desarrollo decimal infinito en el cuál jamás se repite algún tipo de período.
ejemplos:
Al conjunto de los Reales se le conoce también como "El Continuo" ....
Nota:
Toda fracción puede escribirse como decimal, PERO
NO TODO decimal puede escribirse como fracción.
2)
Los números Reales, dijimos, se forman por la unión de los Racionales (Q) y los Irracionales (Q*).
La sola presencia de los Racionales (Q), deja incompleta la Recta Numérica, es decir, si en una recta numérica graficamos Q, que contiene como subconjuntos a IN, INo y Z, la recta estaría llena de hoyos o agujeros .... faltarían infinitos números: Faltarían los Irracionales !!!!
¿ Qué cree Ud., son más los Racionales(Q) o los Irracionales(Q*) ?
3)
Hasta IN, INo, Z y Q, los conjuntos numéricos se llaman ENUMERABLES, porque se pueden hacer corresponder biunívocamente (uno a uno) con los números Naturales (IN) o de contar.
De allí en adelante, es decir, Tanto los Irracionales (Q*), como los Reales ( IR), hablamos de Conjuntos Numéricos NO Enumerables, porque no se pueden hacer corresponder biunívocamente con los Naturales ( IN ).
Esto lo descubrió o al menos lo demostró Cantor.
4)
George Cantor (1845 - 1918): Matemático alemán, de origen ruso, creador de la Teoría Axiomática de Conjuntos, y el primero capaz de expresar formalmente en lenguaje matemático la idea o noción de INFINITO, bajo la forma de un nuevo conjunto numérico, los números Transfinitos.
Las ideas de Cantor acerca del infinito recibieron una crítica generalizada que tal vez agravó su tendencia crónica a la depresión, lo que a su vez le llevó muchas veces a estar internado. Sin embargo su obra se hizo trascendente y fundamental para las matemáticas actuales.
El matemático David Hilbert describió el trabajo de Cantor como "el producto más depurado de genio matemático y uno de los mayores logros de la actividad intelectual pura".
5)
Los números Racionales (Q) son infinitos y también lo son los Reales (R); sin embargo, hay más números Reales que Racionales. Georg Cantor, matemático del siglo XIX, fue el pionero en investigar esta aparente paradoja, remeciendo las bases de la matemática que se conocía al momento: al afirmar que existen distintos tipos de infinitos: algunos mayores que otros.
6)
Infinito: ¡ La PARTE igual al TODO !
Entre los años 1870 y 1880 Cantor y Dedekind iban a operar un cambio REVOLUCIONARIO.
De aquello que se había siempre pensado una imposibilidad: que la parte sea igual al todo, ellos hicieron una propiedad.
Ellos mostraron utilizando la correspondencia biunívoca, que el conjunto de los naturales ( IN: Números de contar ) es tan grande como los pares, por ejemplo, porque se puede hacer una correspondencia biunívoca entre los Naturales y los Pares (o impares).
A este conjunto enumerado (hecho corresponder numéricamente con los naturales) se le llama Infinito Numerable o Enumerable o a veces Infinito Discreto.
De igual forma demostró Cantor que hay tabtos Naturales como Enteros (Z) y Racionales (Q).
¿Pero hay solamente un tipo de Infinito?
¿No se podría, en el infinito, ir más allá de los numerable?
En la imagen, una intervención artística personal a la obra de Max Ernst.
7)
¿Es el numerable el único infinito?
Cantor responde que NO.
La potencia de los números Reales es mayor que el numerable.
En efecto es imposible construir una correspondencia biunívoca entre IN y R.
Es decir, hay infinitamente más puntos en la Recta Numérica que números Naturales (o Cardinales o Enteros, o Racionales).
Tenemos dos Infinitos:
1) El numerable ( IN; INo; Z; Q)
2) el de IR, denominado "El Continuo".
Pero cuidado, de nuevo, por más asombro que le cause: No hay más puntos en todo IR, que en el segmento [0,1].
Pero, ¿Hay otros infinitos más allá del Numerable y del Continuo?
8)
Cantor dice que SÍ, que hay otros infinitos más grandes .... Dice que el conjunto de las partes de un conjunto A, tiene una potencia superior.
El conjunto de todos los subconjunto de IR, posee una INFINITUD MAYOR ....
Podemos partir de IN, luego seguir con Z, Q, Q* y construir sus conjuntos de subconjuntos ....
Hay una infinidad de infinitos.
9)
Dos tipos de Infinitos:
IN: Naturales: Alfa Cero (Infinito Numerable)
INo: Cardinales: Alfa Cero (Infinito Numerable)
Z: Enteros: Alfa Cero (Infinito Numerable)
Q: Racionales: Alfa Cero (Infinito Numerable)
------------------------------------------------------------
Q*: Irracionales: Alfa 1 (Infinito No Numerable)
IR: Reales: Alfa 1 (Infinito No Numerable)
10)
El infinito que a mi me gusta ....
Katsushika Hokusai, uno de los artistas japoneses más conocidos a nivel mundial, realizó cerca de treinta mil obras de arte a lo largo de su carrera. Aunque su estilo dista mucho del arte tradicional japonés, su obra es clave en las historia de la producción artística de este país.
Hokusai nació en 1760, en el seno de una familia de artesanos en la provincia japonesa de Edo. Comenzó a pintar desde que tenía seis años, muy probablemente bajo la tutela de su padre, cuyo trabajo era hacer espejos y decorar los marcos con meticulosas ornamentas. En 1779 publicó sus primeras piezas de ukiyo-e –estampas japonesas que mostraban distintas costumbres– como parte de una serie de impresos sobre teatro Kabuki. Durante su primera etapa creativa su estilo se regía por la tradición japonesa, tanto en técnica como en temática, pero a finales del siglo XVIII adquirió varios grabados calcográficos en cobre hechos en Francia y Holanda, que lo llevaron a explorar con diferentes estilos de Occidente. Esto influyó en los temas que trataba en sus obras, se alejó de los actores Kabuki y los cortesanos para enfocarse en el paisaje y en imágenes cotidianas de la vida en Japón, un cambio fundamental tanto para el artistas como para el género ukiyo-e.
La obra más famosa de Hokusai es Treinta y seis vistas del Monte Fuji, una serie de 36 xilografías realizadas entre 1831 y 1833. En una segunda publicación se añadieron diez xilografías más a la serie en las que el artista japonés retrata al Monte Fuji desde diferentes perspectivas y en distintas condiciones climáticas.
La gran ola de Kanagawa, también conocida como La gran ola, es la pieza más reconocida de la serie y de la carrera de Hokusai. De ésta se realizaron miles de copias, y varias llegaron a manos de coleccionistas europeos. A partir de la década de 1870, La gran ola se volvió muy popular entre artistas y coleccionistas franceses.
lunes, 12 de enero de 2015
PSU en 2do. Medio - 1er Trimestre (Resuelto)
Respuesta:
II y III son Racionales,
Alternativa C)
Fuente: CEPECH
NEM: Segundo Medio.
Eje Temático: I.) Números.
CMO: Conjuntos Numéricos, Racionales, Irracionales
viernes, 9 de enero de 2015
Conjuntos Numéricos - 2do. Medio
La Cultura de los Números o de los Conjuntos Numéricos: ¿Qué
Conjuntos Numéricos conocen?
Desde los albores de los tiempos los números han sido imprescindibles
para el avance de las sociedades humanas, al punto que se puede decir que la
historia de la construcción humana va aparejada a la construcción de los
conjuntos numéricos necesarios para ello. Esto significa que los Conjuntos
Numéricos han evolucionando en el tiempo y por otra parte que, en muchos momentos
de la historia se INVENTARON o DESCUBRIERON otros Conjuntos Numéricos, porque
los que había se tornaban insuficientes.
Las fracciones por ejemplo ya eran usadas por los egipcios mil años
antes de Cristo. Los números negativos por el contrario, entraron mucho más
tardíamente en escena y fueron combatidos con temor, al punto de calificárseles
de absurdos: Al-Khowarizmi, decía que si se obtenía un número negativo “la cosa [incógnita] que te propusieron es
NADA”. Mientras los números negativos eran usados en India en el siglo VI
d.C. (como parte de sus cálculo comerciales), occidente tuvo que esperar hasta
el siglo XVII para tratarlos sin miedo.
Para los griegos el universo se podía expresar en términos de números,
cuando ya en el siglo VI a.C declararon “todo
es número”, es decir, TODO era explicable por medio de las matemáticas.
Desde la geometría los matemáticos se enfrentaron a dos extraños
números:
Euclides, al escribir sobre estos números planteó que eran
INEXPRESABLES o “alogos”. Sin embargo un matemático medioeval interpretó
erróneamente “logos” como razón, por lo que estos números fueron bautizados
como irracionales. Este término es aplicable a cualquier número que no se pueda
escribir como fracción. FINALMENTE: Los números REALES (IR) serán la unión de
los números Racionales (Q) con los Irracionales (Q*): IR = Q U Q*.
lunes, 24 de marzo de 2014
sábado, 8 de marzo de 2014
3/14: Catorce de Marzo : Día Internacional de Pi .... (3,14 ..... )
¿ Qué sabes de Pi ?
10 tips para entender Pi:
1) Pi es el número más famoso de las matemáticas.
2) Pi es un número IRRACIONAL, es decir: NO Racional, es decir (valga la redundancia), NO se puede escribir como una razón, como una fracción de números naturales. Por ejemplo: 0,25 se puede escribir como 1/4 .... pero Pi, que es 3,14 .... NUNCA podrá ser escrito como una razón.
3) Pueblos de la antigüedad sabían de Pí, sabían aproximar su valor por una fracción. Dije Aproximar, porque nunca será en forma exacta una fracción, por lo dicho en 2). Algunos pueblos lo usaban como 22/7 .... en la Biblia se le aproxima a 3.
4) ¿Qué es Pi? El el número de veces que cabe el diámetro de una circunferencia en su perímetro:
5) En babilonia se aproximó Pi por 3,125. Arquímides lo acotó entre 223/71 y 22/7.
6) El matemático Inglés William Jones (1675-1749) introdujo su símbolo, que está en la imagen previa.
7) Los números que forman su parte decimal son INFINITOS y en ellos NO hay NINGUN patrón ordenado, en toda su distribución.
8) Hoy se conocen más de un billón de dígitos de Pi.
9) Akira Haraguchi, un ingeniero japonés jubilado, estableció un record mundial al memorizar cien mil dígitos de Pi que era capaz de recitar .... PLOP! (Es verdad!)
10) Hay un espacio web en donde puedes por ejemplo, poner el número de tu carnet de identidad y el espacio te busca en qué lugar de Pi, está este número:
OJO: Al parecer el enlace está quebrado, pero miren esto, tomado de Microsiervos:
PI Phone Number Search Engine es una página que busca cualquier número que le indiques, especialmente números de teléfono, dentro de los deciminales de π (Pi). La búsqueda se realiza entre los primeros 4.200.000.000 decimales y está limitada a exactamente siete dígitos. Así que puedes buscar teléfonos fijos pero sin prefijo, o móviles sin los tres primeros números de operadora, o tu número de DNI o cualquier otro que se te ocurra si tiene siete dígitos o lo puedes rellenar con ceros.
Con el código fuente en lenguaje C que hay en la página y una secuencia más larga y un servidor más potente se podrían buscar más de siete dígitos.Da que pensar, ¿verdad?
Realmente, ¿están todos los números en PI?
¿Si es así, están todos los decimales del número e en PI? e es un número infinito, PI contiene a e.
¡Qué comedura de tarro! Es lo que tienen las mates.
.........
11) y algo muy importante: Pi es Trascendente, es decir, como dicen los matemáticos elegantes, Pi NO es la raíz (solución) de ningún polinomio con coeficientes enteros.
martes, 11 de febrero de 2014
Suscribirse a:
Entradas (Atom)