miércoles, 2 de septiembre de 2015
En torno a la geometría ....
lunes, 31 de agosto de 2015
Desafío - Teorema de Pitágoras - 7mo a 2do. Medio (Ejercicio Propuesto)
¿Hay otros tipos de GEOMETRIA además de la Plana o de Euclides?
Hay otros tipos de Geometría, Posteriores a la Plana o de Euclides, que fueron construyéndose poco a poco para responder a las necesidades de la ciencia, a las exigencias para comprender la naturaleza .... algunas de ellas ....
1) Geometría del Espacio o Estereometría (Contemporánea de la Plana)
2) Geometría Afín
3) Geometría Analítica
4) Geometría Descriptiva
5) Geometría Métrica
6) Geometría Integral
7) Geometría Proyectiva
8) Geometría Diferencial
9) Geometría Hiperbólica
10) Geometría Elíptica
11) Geometría Esférica
12) Geometría Fractal
sábado, 29 de agosto de 2015
A veces los chicos y chicas ....
(*) DISCULPAS POR LA EXPRESIÓN!
LINK: Materia Geometría 2do Medio Exámenes Libres
lunes, 3 de agosto de 2015
Historia de la GEOMETRIA - Tomado de Profesor en línea
Historia de la Geometría |
 |
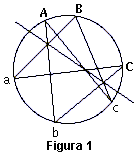
| Pitágoras |
 |
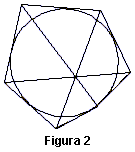
| Apolonio de Perga |
 |
 |
 |
 |
| Carl Fiedrich Gauss |
 |
| János Bolyai |
 |
| Arthur Cayley |
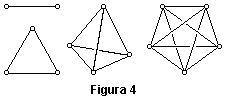 |
martes, 21 de julio de 2015
Jugan con Construcciones Geométricas ONLINE, en Inglés básico
domingo, 24 de mayo de 2015
Medidas de Arco y Sector Circular - 8avo., lo que viene!
domingo, 12 de abril de 2015
que onda con la geometría?
martes, 17 de marzo de 2015
A los 4 añitos ....
Los niños de cuatro años ya tienen nociones de geometría euclidiana
Un estudio liderado por investigadores de la Universidad de Harvard (EEUU) ha revelado que los niños de cuatro años poseen habilidades que podrían representar una comprensión temprana de la geometría euclidiana. El trabajo ha analizado en niños la relación entre su sentido de la orientación, su capacidad de analizar formas y su interpretación de mapas simbólicos.
- Más información sobre:
- geometría euclidiana
- cuatro años
- niños
- PNAS
SINC | 13 agosto 2013 15:36


Los niños que mejor manejaban distancias y direcciones ubicaron bien el peluche en el triángulo sin esquinas. / Moira Dillon
Los adultos humanos de diferentes culturas comparten intuiciones sobre puntos, líneas y figuras de la geometría euclidiana. Ya desde niños desarrollan nociones tempranas para orientarse en el espacio y analizar la forma de los objetos, pero ¿cómo llegan al pensamiento euclidiano?
Según un estudio que se presenta esta semana en la revista Proceedings of the National Academy of Sciences (PNAS), a los cuatro años de edad los humanos ya poseen habilidades que demuestran una comprensión temprana de la geometría euclidiana.
El trabajo, liderado por investigadores de la Universidad de Harvard, ha estudiado en niños la relación entre su sentido de la orientación, su capacidad de analizar formas y su interpretación de mapas simbólicos.
Según el artículo, muchos animales, incluidos los humanos, poseen un entendimiento innato de la geometría simple. Reconocen objetos mediante ángulos y longitudes relativas, y se desplazan por su entorno empleando nociones de distancias y direcciones. Unidas, estas dos representaciones geométricas básicas podrían formar la base del pensamiento abstracto geométrico exclusivo de los humanos.
Según este nuevo trabajo, los niños no parecen integrar tales nociones; sin embargo, sí hacen un uso flexible de la geometría abstracta en la lectura de mapas, lo que podría llevar a la posterior construcción de la geometría euclidiana.
Uno de los experimentos llevados a cabo en el estudio consistió en vendar los ojos de los niños participantes y hacer que giraran para ver cómo se orientaban, tras destaparles los ojos, en un área con forma rectangular. También se les hizo pasar un test de ordenador que evaluaba su habilidad para reconocer distintas formas geométricas.
Como animales en su hábitat
Después se situó a los niños en el centro de dos áreas con forma de triángulo. En uno de los dos escenarios del experimento, el triángulo tenía sus tres lados pero le faltaban todas las esquinas. En el otro, le faltaban los lados y solo tenía las tres esquinas. Los investigadores mostraron a todos los niños los mismos mapas para que localizaran ciertos puntos en el borde del triángulo donde debían colocar un juguete de peluche.
Moira Dillon, coautora del estudio, explica que los niños que mejor manejaban distancias y direcciones ubicaron bien el peluche en el triangulo sin esquinas. En cambio, los más hábiles en las pruebas de reconocimiento de formas geométricas en el ordenador obtuvieron resultados superiores en el triángulo compuesto solo por esquinas.
El trabajo sugiere que las habilidades geométricas tempranas son las mismas que las que usan los animales para moverse en su hábitat. Según los investigadores, en torno a los dos años y medio, los niños empiezan a ser capaces de abstraer esos principios para leer mapas adaptando a cada situación el tipo de información que emplean, como en el caso de los dos escenarios triangulares.
Referencia bibliográfica:
Moira R. Dillon, Yi Huang, Elizabeth S. Spelke. "Core foundations of abstract geometry”. Proceedings of the National Academy of Sciences (PNAS), 12 de agosto de 2013.
lunes, 16 de marzo de 2015
Maravillosoooooooo !!!!!!! (Colabora Daniela Saldías)
martes, 25 de noviembre de 2014
Geometría en Inglés !
martes, 8 de julio de 2014
Construcciones Geométricas versus Construcciones Mecánicas - 7mo.
lunes, 16 de junio de 2014
Bisectrices y Circunferencia Inscrita - 7mo. (Hoja Dinámica de Prueba con GEOGEBRA)
Construir Simetral a Trazo con Geogebra - 7mo.
¿Qué es una Simetral? 1: Simetral 1
¿Qué es una Simetral? 2: Simetral
Recordamos que la Simetral a un trazo es una perpendicular en su punto medio:
Paso 1:
Paso 2:
Paso 3:
Paso 4:
Paso 5: Trazamos una recta por los puntos F y G, que es la Simetral, porque pasa por el punto medio y es perpendicular al trazo AC.:



























