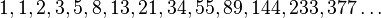Mostrando entradas con la etiqueta Aula Poética. Mostrar todas las entradas
Mostrando entradas con la etiqueta Aula Poética. Mostrar todas las entradas
miércoles, 6 de mayo de 2015
domingo, 21 de septiembre de 2014
jueves, 18 de septiembre de 2014
lunes, 8 de septiembre de 2014
lunes, 28 de julio de 2014
a veces por las noches ....
a veces por las noches ....
==================
a veces por las noches
el suave rocío de Arrieta, su viento gélido, su nieve
se levantan a tejer Matemáticas
quizás es Francisco Varela, con su sonrisa el que entrama
quizás es su meditación autopoiética .... la que nos enactúa
y nos deja regalos, coloridos, copiosos
cochayuyos cantores también revoltosos
barcazas, rabeles y ajos chilotes ....
pelotas de futbol, grabados y risas ....
edificios de cartón, banderas budistas, sombreros ....
ecuaciones, escarchas, cuerpos abrazados ....
pehuenes, pifilcas, amores de patio ....
la huerta, los juegos,
el sol y las manos ....
==================
a veces por las noches
el suave rocío de Arrieta, su viento gélido, su nieve
se levantan a tejer Matemáticas
quizás es Francisco Varela, con su sonrisa el que entrama
quizás es su meditación autopoiética .... la que nos enactúa
y nos deja regalos, coloridos, copiosos
cochayuyos cantores también revoltosos
barcazas, rabeles y ajos chilotes ....
pelotas de futbol, grabados y risas ....
edificios de cartón, banderas budistas, sombreros ....
ecuaciones, escarchas, cuerpos abrazados ....
pehuenes, pifilcas, amores de patio ....
la huerta, los juegos,
el sol y las manos ....
lunes, 7 de julio de 2014
Microcuento Matemático - Fernando Williams
Quién no ha tenido pesadillas con las matemáticas... escapar de hipotenusas-robots que tratan de atraparte mientras uno corre y corre por escaleras de fibonacci hechas de números imaginarios.
de Wikipedia (con permiso):
En matemáticas, la sucesión de Fibonacci (a veces mal llamada serie de Fibonacci) es la siguiente sucesión infinita de números naturales:
A los elementos de esta sucesión se les llama números de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la flora de la alcachofa, las inflorescencias del brécol romanescu y en el arreglo de un cono.
de Wikipedia (con permiso):
En matemáticas, la sucesión de Fibonacci (a veces mal llamada serie de Fibonacci) es la siguiente sucesión infinita de números naturales:
A los elementos de esta sucesión se les llama números de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la flora de la alcachofa, las inflorescencias del brécol romanescu y en el arreglo de un cono.
jueves, 12 de junio de 2014
Caen fractales sobre la escuela ....
Hoy, magia ....
en el rito de saludo a la PachaMama,
algunas chicas(os) del 7mo. pidieron que NEVARA ....
y así fue y ....
copos de nieve saltarines salieron a abrazar a los fractales
que venían disfrazados de NIEVE
que caían ....
Ciertamente Todas estas figuras quedan muy bien como adornos de Navidad pero sólo algunas de ellas se podrían encontrar en copos de nieve de verdad.
La respuesta es simple ... 1, 2, 3 (Las primeras 3).
Si optaste por la primera segunda y tercera figuras ...
has acertado !
En matemáticas, la nieve se puede simular por medio del conocido Copo de Nieve de Koch, que como ves tiene simetría hexagonal ..... en la medida que avanzamos en la iteraciones de generación ....
El copo de nieve de Koch, también llamado estrella de Koch, es una curva cerrada continua (no diferenciable para los matemáticos mayores), descrita por el matemático sueco Helge von Koch en 1904 en un artículo titulado "Acerca de una curva continua que no posee tangentes y obtenida por los métodos de la geometría elemental".
en el rito de saludo a la PachaMama,
algunas chicas(os) del 7mo. pidieron que NEVARA ....
y así fue y ....
copos de nieve saltarines salieron a abrazar a los fractales
que venían disfrazados de NIEVE
que caían ....
(Crédito de la Foto: Francisca, educadora de Inglés)
has acertado !
La razón es que esas son las únicas figuras del grupo con simetría hexagonal . Esto quiere decir que si giramos la figura 1/6 (60°), una sexta parte de una vuelta completa como si fuera una rueda, acabamos con una nueva orientación indistinguible de la posición inicial (aparte de los pequeños defectos añadidos a los dibujos para hacerlos parecer más reales).
Los matemáticos y cristalógrafos usan el término "eje de orden 6" para describir este tipo de simetría.
El cuarto y el quinto dibujo tienen simetrías diferentes. El cuarto presenta un eje de orden 8 (simetría octogonal), mientras que el quinto tiene un eje de orden 5 (simetría pentagonal).
El caso es que los cristales de nieve siempre crecen formando figuras hexagonales. Las formas son infinitas, cada cristal es único, pero la simetría (tema desde cuarto básico) de todos ellos es la misma.
En matemáticas, la nieve se puede simular por medio del conocido Copo de Nieve de Koch, que como ves tiene simetría hexagonal ..... en la medida que avanzamos en la iteraciones de generación ....
El copo de nieve de Koch, también llamado estrella de Koch, es una curva cerrada continua (no diferenciable para los matemáticos mayores), descrita por el matemático sueco Helge von Koch en 1904 en un artículo titulado "Acerca de una curva continua que no posee tangentes y obtenida por los métodos de la geometría elemental".
En lenguaje actual, diríamos que es una curva fractal. Su construcción más simple se realiza mediante un proceso iterativo que se inicia partiendo en tres un segmento de recta e insertando dos más en el tercero medio a manera de un triángulo equilátero, el proceso se repite infinidad de veces (Wikipedia).
miércoles, 23 de abril de 2014
tengo las mismas dudas de Gabriela Mistral ....
(Un homenaje a mis panas de la Escuela Francisco Varela, porque los veo luchando, pensando, debatiendo internamente como HACER MEJOR .... para que todos(as) seamos mejores ....)
Tengo las mismas dudas de Gabriela Mistral ....
No, no puede ser, ella no era un intento matemático,
pero seguro pensaba y pensaba bajo su cielo del Elqui
como enfrentar el aula de sus peques
para lograr en(con) ellos el ansiado viaje ....
Mañana paso Volúmenes en 1ro. Medio
-Tedioso es pasar un tremendo formulario-
Pero no!, voy a usar las lentejas para mostrar que un cono de igual base y altura que un cilindro,
puede ser contenido tres veces dentro de éste ....
¿Pero será suficiente para que no se queden dormidos? .... NO!
Es un tanto pueril el juego anterior, pero de seguro -si olvidan la fórmula-
nunca olvidarán la imagen de las tres veces ....
Estoy como Gabriela, pensando bajo el cielo con varios lápices afilados, para que no se me escapen los versos ....
Ah .... se me ocurre, que para que entiendan en imágenes, el volumen de un cilindro,
repitiendo MUCHÍSIMAS veces el área de un círculo, tantas como sea su altura,
llevar unos círculos que apilándose, formen un pequeño cilindro, si, eso, eso .... siiiiiiiiii !!!!!!!
y, para eso me sirven los cartones de las cajas de yerbas y las pastas dentales que acumulaba hace rato ....
¿Y si me vuelco a la historia y les hablo del Método de Exhaución, la exhaución de Arquímdes, con el cual logró aproximar la longitud de una circunferencia, agotando ajustes de polígonos regulares en el círculo?
Exhaución viene de Exhauto, YO estoy exhauto,
y su raíz en latín viene de "Agotamiento" .... yo estoy agotado pero pensando,
Gabriela dice que ella escribe con una rapidez vertical ,,,, como piedras que bajan verticalmente por un acantilado .... eso me pasa ahora, se me ocurren ideas que fluyen con rapidez vertical .... se llena mi cabeza ....
Y si una imagen como la siguiente viniera sobre ellos como un pájaro rasante ....
Porque al final, tras la invención del Cálculo, lo que se hizo ESENCIALMENTE, fue ni más ni menos la idea de Arquímides, ahora con el recurso del uso de los diferenciales (dx) ....
Y si les digo, miren, en la Universidad, algún día -si siguen una carrera científica,- tendrán que ver esto:
Tengo las mismas dudas de Gabriela Mistral ....
No, no puede ser, ella no era un intento matemático,
pero seguro pensaba y pensaba bajo su cielo del Elqui
como enfrentar el aula de sus peques
para lograr en(con) ellos el ansiado viaje ....
Mañana paso Volúmenes en 1ro. Medio
-Tedioso es pasar un tremendo formulario-
Pero no!, voy a usar las lentejas para mostrar que un cono de igual base y altura que un cilindro,
puede ser contenido tres veces dentro de éste ....
¿Pero será suficiente para que no se queden dormidos? .... NO!
Es un tanto pueril el juego anterior, pero de seguro -si olvidan la fórmula-
nunca olvidarán la imagen de las tres veces ....
Estoy como Gabriela, pensando bajo el cielo con varios lápices afilados, para que no se me escapen los versos ....
Ah .... se me ocurre, que para que entiendan en imágenes, el volumen de un cilindro,
repitiendo MUCHÍSIMAS veces el área de un círculo, tantas como sea su altura,
llevar unos círculos que apilándose, formen un pequeño cilindro, si, eso, eso .... siiiiiiiiii !!!!!!!
¿Y si me vuelco a la historia y les hablo del Método de Exhaución, la exhaución de Arquímdes, con el cual logró aproximar la longitud de una circunferencia, agotando ajustes de polígonos regulares en el círculo?
Exhaución viene de Exhauto, YO estoy exhauto,
y su raíz en latín viene de "Agotamiento" .... yo estoy agotado pero pensando,
Gabriela dice que ella escribe con una rapidez vertical ,,,, como piedras que bajan verticalmente por un acantilado .... eso me pasa ahora, se me ocurren ideas que fluyen con rapidez vertical .... se llena mi cabeza ....
Y si una imagen como la siguiente viniera sobre ellos como un pájaro rasante ....
Y si les digo, miren, en la Universidad, algún día -si siguen una carrera científica,- tendrán que ver esto:
Que es exactamente la bellísima fórmula del área de una ESFERA ....
No sé ,,,, no me atrevo ,,,, ellos están muy concretos ,,,,
pero, por qué no volar un poco
¿y hacer -por un segundo- matemáticas de futuro?
Como dice Gabriela .... "Escribir me suele alegrar!"
=====================================
(Gracias por el poema compuesto de Gabriela, Verito)
domingo, 13 de abril de 2014
Palomas Positivas: Aula Poética - Números Enteros - 7mo y 1ro. Medio
Recta Numérica ..... (de los Enteros, Conjunto Z)
O sea
que si asignamos a una paloma
ser el número CERO,
¿algunas de ellas serán POSITIVAS?
lunes, 17 de febrero de 2014
lo vuelvo a mostrar, poque me parece maravilloso .... (tomado de Aula Poética)
Construcción Geométrica:
Construya varias líneas paralelas
y sobre ellas puntos azarosos
-pero que esta vez .... vuelen-
miércoles, 12 de febrero de 2014
martes, 11 de febrero de 2014
Lineas Paralelas .... como acción poética (tomado de Aula Poética)
Construcción Geométrica:
Construya varias líneas paralelas
y sobre ellas puntos azarosos
-pero que esta vez .... vuelen-
Suscribirse a:
Entradas (Atom)