"Para Malaguzzi, todas las criaturas, en todas y cada una de las culturas, son inteligentes" (A.H.)
lunes, 25 de enero de 2016
domingo, 24 de enero de 2016
Comando Geogebra para Graficar Por Partes - 1ro. Medio 2016 - EFV
En Primero Medio, en el nuevo programa (actualizado) piden Funciones Lineal y Afín. Lo más pertinente sería graficar dos planes reales de Teléfono y comparar la mejor opción de pago, adecuada a nuestro estilo de consumo, para lo cual se hará importante graficar funciones definidas por Partes (o Tramos).
Acá la forma de utilizar el comando en Geogebra:
Función Tipo (aunque esta no es de teléfonos, porque no hay consumos negativos)
Comando:
Grafo Final:
Acá la forma de utilizar el comando en Geogebra:
Función Tipo (aunque esta no es de teléfonos, porque no hay consumos negativos)
Comando:
Grafo Final:
Etiquetas:
Conando Geogebra,
Función Afín,
Funciones,
Funciones por Partes o Tramos,
Geogebra
viernes, 22 de enero de 2016
Numero de calzado y edad .... Esto es Matemagia!
martes, 12 de enero de 2016
jueves, 7 de enero de 2016
Qué es GOOGOL y GOOGOLPLEX ???? - 7mo.
Para tratar de despertar la curiosidad de los niños y niñas, el matemático norteamericano Edwar Kasner (1878-1955) escribió en una pizarra, en la visita a la escuela de su sobrino, el número:
Par mostrar cuando grande era, alineó un 1 seguido de 100 ceros
(porque esto es la definición de 10 elevado a 100):
10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Un número muy grande para el que pidió a su sobrino que le pusiera un nombre.Su sobrino le dijo de inmediato: ¡llamémosle Googol!
Cuando los fundadores de la empresa GOOGLE, le pusieron el nombre a su empresa, utilizaron la idea del Googol, para significar que su motor ayudaba a acceder a una "infinita" red. Pero escribieron mal el nombre.
Pero Kasner no se contentó con el Googol, inventó el GoogolPLEX:
Par mostrar cuando grande era, alineó un 1 seguido de 100 ceros
(porque esto es la definición de 10 elevado a 100):
10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Un número muy grande para el que pidió a su sobrino que le pusiera un nombre.Su sobrino le dijo de inmediato: ¡llamémosle Googol!
Cuando los fundadores de la empresa GOOGLE, le pusieron el nombre a su empresa, utilizaron la idea del Googol, para significar que su motor ayudaba a acceder a una "infinita" red. Pero escribieron mal el nombre.
Pero Kasner no se contentó con el Googol, inventó el GoogolPLEX:
y para hacernos una leve imagen de lo que este número significa, En caso de que pudiésemos escribir lo manualmente, poniendo un uno seguido de ceros -ubicados cada medio centímetro- la longitud de esta escritura sería SUPERIOR al RADIO del Universo observable, que es:
(47 mil millones de años luz ....)
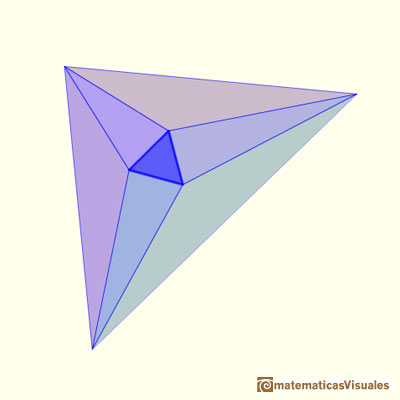
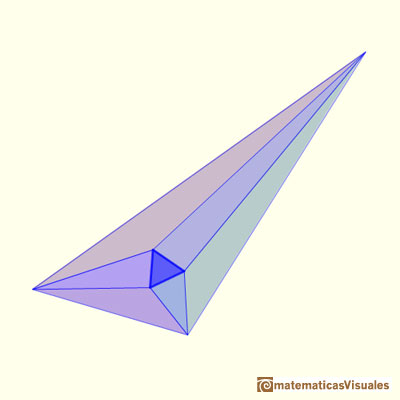
Teorema de Morley - Demostrado por John Conway - Tomado de Matermáticas Visuales
Demostración deJohn Conway del teorema de Morley.
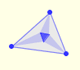
Los tres puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera son los vértices de un triángulo equilátero (Triángulo de Morley).
Este teorema fue un sorprendente descubrimiento que hizo Frank Morley (hacia 1899).
Conway escribe: "El teorema de Morley es reconocido como un teorema que es realmente difícil de probar. Es muy sencillo de formular, pero muy difícil de probar"(John Conway).
Se considera que la demostración de John Conway es la más sencilla y es un buen ejemplo de "demostración de atrás para adelante".
"Podemos probar el teorema de Morley de un modo sencillo como sigue. Primero, tienen que decirme la medida de los tres ángulos A, B, C, de su triángulo original. Recordamos que tienen que sumar 180 grados. Este es el plan: Voy a empezar con un triángulo equilátero de algún tamaño
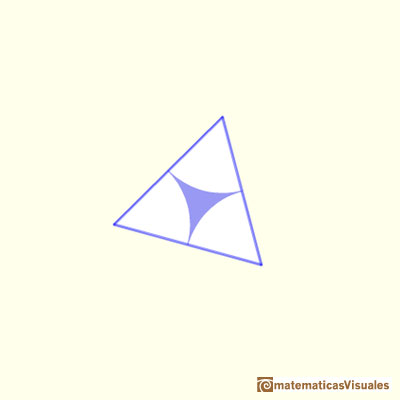
y vamos a construir otros seis triángulos alrededor de él y los vamos a pegar juntos para crear un triángulo cuyos ángulos son A, B y C, justamente igual que los suyos; por lo tanto, para algún tamaño adecuado del triángulo equilátero, mi construcción reproducirá exactamente su triángulo original; además el método de construcción probará que si trisecamos los ángulos de su triángulo encontraremos un triángulo equilátero en el medio. Estas son las seis piezas triangulares que construiremos alrededor del triángulo equilátero" (John Conway)
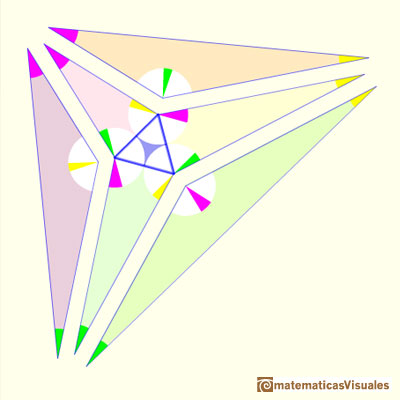
"Para entender la demostración correctamente, tenemos que pensar los seis nuevos triángulos como piezas que vamos a definir, empezando por el triángulo equilátero, con la ayuda de los valores A, B y C iniciales. La figura anterior es nuestro destino, no el punto de partida.
Construiremos los seis nuevos triángulos primero definiendo su forma y después definiremos su tamaño. Para definir las formas de estos seis triángulos tenemos que fijar sus ángulos." (John Conway)
Los ángulos blancos miden 60 grados. Podemos comprobar que los ángulos de cada triángulo suman 180 grados.
Estas son las formas de los primeros tres triángulos:
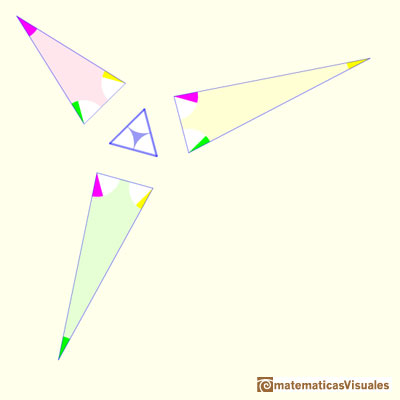
Para fijar los tamaños de estos tres triángulos hacemos que la longitud de uno de los lados sea igual a la del triángulo equilátero.
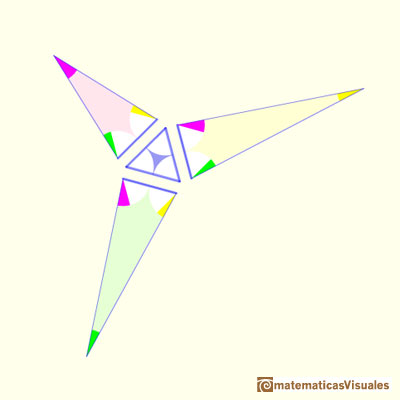
Podemos pegar estos tres triángulos al triángulo equilátero:
Para fijar las tamaños de los tres triángulos obtusos introducimos dos segmentos iguales desde el vértice opuesto al lado largo de cada triángulo ("un poco al estilo como si trazáramos perpendiculares", escribe Conway). Estas líneas forman triángulos isósceles.
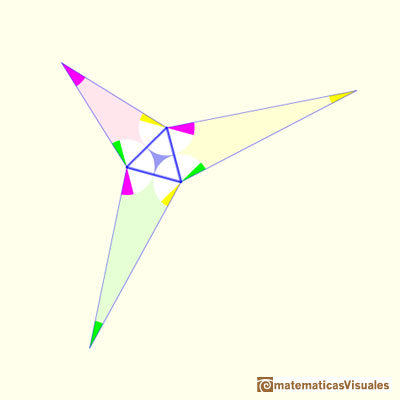
Podemos fijar el tamaño de estos triángulos haciendo que estos segmentos tengan la misma longitud que el lado del triángulo equilátero.
Pero ¿cómo se dibujan estos segmentos? Mirando las figuras podemos entender los ángulos que se forman.
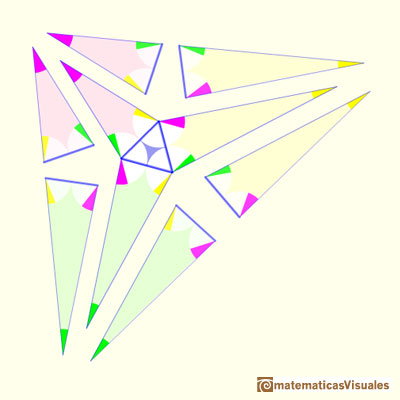
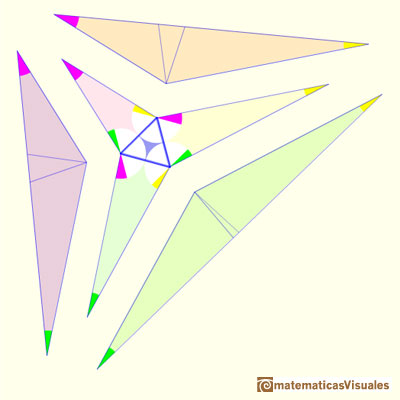
Desdoblando esos tres triángulos obtenemos seis triángulos. Por parejas son iguales a uno de los tres triángulos que construímos primero. Es decir, de los nueve triángulos que tenemos alrededor del equilátero, los tres que comparten el color son iguales (o quizás imágenes especulares). Nos fijamos que tienen tres ángulos iguales y también tienen igual un lado (que es igual al lado del triángulo equilátero).

Podemos comprobar que las medidas de los ángulos son correctas y que los ángulos alrededor de cada vértice interno suman 360 grados.
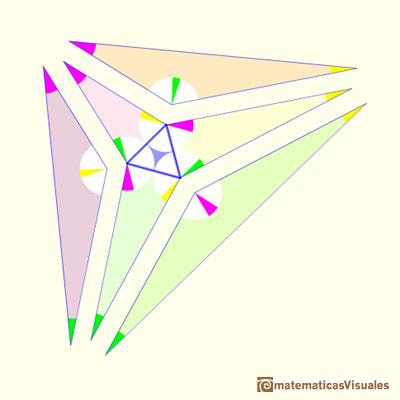
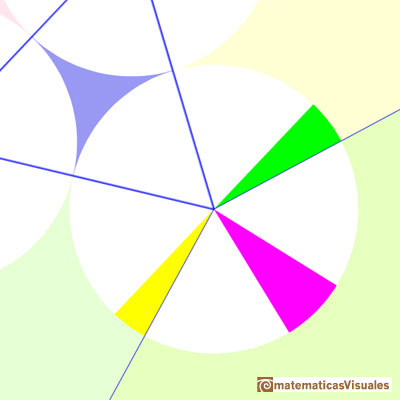
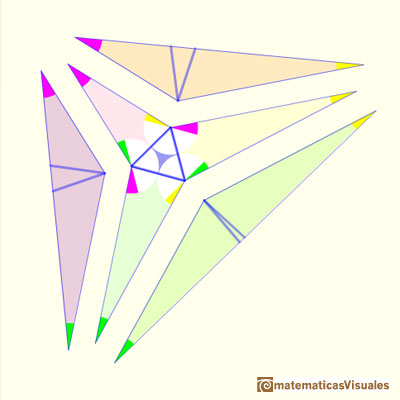
"Entonces, pegando las siete piezas juntas he conseguido un triángulo con los ángulos que usted me ha proporcionado, para el que el teorema de Morley es cierto.
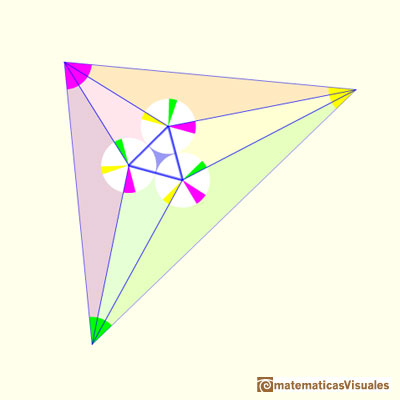
Es decir, el teorema de Morley es verdad para su triángulo y para cualquier triángulo que pudiéramos haber escogido." (John Conway)
Etiquetas:
Conway Horton John,
Matemáticas Visuales,
Teorema de Morley
Infinito
No es en el firmamento estrellado,
ni en el esplendor de las corolas
donde se ve en toda su perfección
la revelación
de lo infinito en lo finito
-motivo de toda creación-,
sino en el alma humana.
Rabindrânath Tagore.
Sâdhanâ
Etiquetas:
Infinito,
Poesía y Matemáticas,
Tagore
miércoles, 6 de enero de 2016
A ver esa mente ....
Otra Prueba Visual ....
Chistes Matemáticos
Demostración Visual
Nuevos Elementos Químicos Sintéticos o Creados por el ser humano.
Cuatro nuevos elementos químicos se han añadido a la tabla periódica, completando así la séptima fila de la misma. Se trata de cuatro elementos químicos superpesados (113, 115, 117 y 118) que han sido descubiertos por científicos de Japón, Rusia y Estados Unidos. Son los primeros en ser añadidos a la tabla desde que en 2011 se añadieron los elementos 114 y 116.
Los cuatro fueron verificados el pasado 30 de diciembre por la Unión Internacional de Química Pura y Aplicada (IUPAC, por sus siglas en inglés), la organización mundial que rige la nomenclatura química, su terminología y su medición, con sede en los Estados Unidos, según informa el diarioThe Guardian.
IUPAC anunció que un equipo ruso-estadounidense de científicos del Joint Institute for Nuclear Research de Dubna (Rusia), y del Lawrence Livermore National Laboratory en California (Estados Unidos), habían aportado las pruebas suficientes para reclamar el descubrimiento de los elementos 115, 117 y 118 .
No obstante, el IUPAC otorgó el crédito por el descubrimiento del elemento 113 a un equipo de científicos del Instituto Riken de Japón, a pesar de que también éste había sido reclamado por los rusos y por los estadounidenses.
El director de la investigación japonesa, Kosuke Morita, ha anunciado tras la noticia que ahora su equipo planea "mirar hacia el territorio desconocido del elemento 119 y más allá".
Por su parte, el premio Nobel de Química, el japonés Ryoji Noyori ha señalado sobre el descubrimiento: "Para los científicos esto es de mayor valor que una medalla de oro olímpica".
Los elementos suelen ser nombrados oficialmente por los equipos que los descubren en los próximos meses. El elemento 113 será el primer elemento en ser nombrado en Asia.
"IUPAC ha iniciado el proceso de formalización de los nombres y de los símbolos para estos elementos, que han sido nombrados temporalmente como 'ununtrium', ('Uut' o elemento 113), 'ununpentium' ('Uup', element 115), 'ununseptium' ('Uus', element 117), and 'ununoctium' ('Uuo', element 118)", explica.
Los nuevos elementos pueden ser nombrados con un concepto mitológico, un mineral, un lugar en un país, una propiedad o un científico.
Los cuatro elementos nuevos, todos hechos por el hombre, fueron descubiertos por golpear núcleos más ligeros entre sí y por la consiguiente descomposición de los elementos superpesados radiactivos.
Al igual que otros elementos superpesados que pueblan el final de la tabla periódica, sólo existen por fracciones de segundo antes de desintegrarse en otros elementos.
Etiquetas:
Nuevos Elementos Químicos,
Química,
Química y Matemáticas
Alejandría, la ciudad de Alejandro Magno.
¿Por qué estudiar Alejandría y Alejandro Magno?
Porque Alejandría fue el centro comercial y cultural más significativo del Mediterránbeo oriental, lugar donde florecieron las matemáticas.
Tomado de:
Hombres y mujeres que hicieron historia.
ALEJANDRO MAGNO
Aguilar Colecciones
Autora: Mabel Pagano.
=================
Hacia fines del año 332 a.C. Alejandro partió desde Menfis, y comenzó a bajar por el cauce del Nilo. Navegó esas aguas durante algunos días hasta que se detuvo al oeste del delta, en las cercanías del lago Marcotis. Allí había un poblado llamado Rakotis, que se hallaba habitado por una comunidad de pescadores.
Observó que se trataba de un lugar privilegiado: protegido de las crecientes del río, cerca del cauce como para contar con la posibilidad de un rápido acceso al puerto y, en consecuencia, a las mercaderías e insumos que por él llegaban.
Después de recorrer el emplazamiento, en compañía de los arquitectos e ingenieros que había llevado consigo, decisió que era un sitios ideal para establecer una ciudad. Así fue como, en enero del año 331 a.C., fundó Alejandría, que rápidamente iba a convertirse en el centro comercial y cultural más importante del Mediterráneo oriental.
La ciudad estaba situada frente a la isla de Faros, la que, gracias a algunas obras posteriores, quedaría comunicada con ella por un dique.
Dinócrates de Rodas, el arquitrecto y urbanista griego que cumplía funciones de asesor téncnico de Alejandro, se ocupó del trazado de la ciudad. Distintos estudios coinciden en la descripción: dividida en cinco distritos, tenía una plaza, una calle mayor de 30 metros de ancho y 6 kilómetros de largo, con vías paralelas y perpendiculares, cruzándose siempre en ángulo recto. Se construyeron barrios cuyas calles tenían conductos de agua por cañerías. Cleomenes de Naucratis fue el hombre elegido por el rey para ocuparse de la administración de la nueva ciudad, cuando el partió hacia la conquista de Persia.
La construcción del faro a cargo de Dinócrates posibilitó la creación de dos puertos: el más importante, el Gran Puesto, hacia el Este, y el Puerto del Buen Regreso, al Oeste. A sus muelles llegaban barcos provenientes del Mediterráneo y del Atlántico, cargados de distintas mercaderías. El faro, construido por el arquitecto Sóstrato de Cnido por orden de Ptolomeo II en 280 a.C., que fue coniderado como una de las Siete Maravillas en la Antiguedad, guió el rumbo de los navegantes hasta 1340, cuando fue destruido.
"Estaba tan decidido a emprender las obras que deambuló por el emplazamiento, arrastrando tras de si a arquitectos e ingenieros y señalando las situaciones de la plaza del mercado, de los templos de los dioses griegos y egipcios, de la vía real. Un hombre listo se percató de que Alejandro Magno no tenía tiza para marcar y le ofreció harina, que el macedonio aceptó. Los pájaros se alimentaron de ella, por lo cual los adivinos previnieron que la ciudad prosperaría y daría de comer a muchos forasteros, predicción que Alejandría sigue cumpliendo. En algún momento de sus impacientes avances debió de cruzar el amplazamiento de su propia tumba, relata Mary Renault en su obrs ya citada.
Porque Alejandría fue el centro comercial y cultural más significativo del Mediterránbeo oriental, lugar donde florecieron las matemáticas.
Tomado de:
Hombres y mujeres que hicieron historia.
ALEJANDRO MAGNO
Aguilar Colecciones
Autora: Mabel Pagano.
=================
Hacia fines del año 332 a.C. Alejandro partió desde Menfis, y comenzó a bajar por el cauce del Nilo. Navegó esas aguas durante algunos días hasta que se detuvo al oeste del delta, en las cercanías del lago Marcotis. Allí había un poblado llamado Rakotis, que se hallaba habitado por una comunidad de pescadores.
Observó que se trataba de un lugar privilegiado: protegido de las crecientes del río, cerca del cauce como para contar con la posibilidad de un rápido acceso al puerto y, en consecuencia, a las mercaderías e insumos que por él llegaban.
Después de recorrer el emplazamiento, en compañía de los arquitectos e ingenieros que había llevado consigo, decisió que era un sitios ideal para establecer una ciudad. Así fue como, en enero del año 331 a.C., fundó Alejandría, que rápidamente iba a convertirse en el centro comercial y cultural más importante del Mediterráneo oriental.
La ciudad estaba situada frente a la isla de Faros, la que, gracias a algunas obras posteriores, quedaría comunicada con ella por un dique.
Dinócrates de Rodas, el arquitrecto y urbanista griego que cumplía funciones de asesor téncnico de Alejandro, se ocupó del trazado de la ciudad. Distintos estudios coinciden en la descripción: dividida en cinco distritos, tenía una plaza, una calle mayor de 30 metros de ancho y 6 kilómetros de largo, con vías paralelas y perpendiculares, cruzándose siempre en ángulo recto. Se construyeron barrios cuyas calles tenían conductos de agua por cañerías. Cleomenes de Naucratis fue el hombre elegido por el rey para ocuparse de la administración de la nueva ciudad, cuando el partió hacia la conquista de Persia.
La construcción del faro a cargo de Dinócrates posibilitó la creación de dos puertos: el más importante, el Gran Puesto, hacia el Este, y el Puerto del Buen Regreso, al Oeste. A sus muelles llegaban barcos provenientes del Mediterráneo y del Atlántico, cargados de distintas mercaderías. El faro, construido por el arquitecto Sóstrato de Cnido por orden de Ptolomeo II en 280 a.C., que fue coniderado como una de las Siete Maravillas en la Antiguedad, guió el rumbo de los navegantes hasta 1340, cuando fue destruido.
"Estaba tan decidido a emprender las obras que deambuló por el emplazamiento, arrastrando tras de si a arquitectos e ingenieros y señalando las situaciones de la plaza del mercado, de los templos de los dioses griegos y egipcios, de la vía real. Un hombre listo se percató de que Alejandro Magno no tenía tiza para marcar y le ofreció harina, que el macedonio aceptó. Los pájaros se alimentaron de ella, por lo cual los adivinos previnieron que la ciudad prosperaría y daría de comer a muchos forasteros, predicción que Alejandría sigue cumpliendo. En algún momento de sus impacientes avances debió de cruzar el amplazamiento de su propia tumba, relata Mary Renault en su obrs ya citada.
Etiquetas:
Alejandría,
Alejandro Magno,
Biblioteca de Alejandría,
Faro de Alejandría
lunes, 4 de enero de 2016
Yo aprendo en "La Escuela Aprende".
Hoy tuvimos una muy buena charla introductoria del Método Singapur en Chile.
Fue dada por la educadora Daniela Goic, del colegio Pedro de Valdivia.
Daniela nos cuenta de que el Método Singapur se empezó a testear en colegios bilingues en el año 2009 -en Chile- y que su aplicación a le educación pública fue desde el año 2011. Ella lo practica desde el 2010.
Daniela nos aclara que la suya será un intervención no teórica sino más bien centrada en pequeñas prácticas que trae de su práctica cotidiana. Daiela nos muestra material concreto: pequeños cubos apilables o montables (de unidades para formar decenas); bloques de decenas (para formar centenas); bloques de centenas para formar unidades de mil; balanzas para adiciones, etc.
Nos habla de que en este método se usa la triada CO-PI-SI (COncreto - PIctórico - SImbolico ó Abstracto), heredada de Brunner, que realza el flujo desde lo enactivo a lo abstracto y que sin embargo tiene la abertura a que los chicos y chicas puedan comenzar en cualquiera de sus estadios o transitar libremente entre ellos.
Nos muestra que tras utilizar los pequeños cubos montables, para pasar de las unidades a las decenas, los chicos y chicas superan los ámbitos numéricos del MINEDUC rápidamente, por ejemplo donde se sugiere ir del 0 al 40, los niños y niñas alcanzan fácilmente del 0 al 100, lo que viene de la riqueza de trabajar con elementos concretos.
Nos dice que una de las grandes diferencias con la educación tradicional proviene de que -por la propia utilización de cubos montables- no se usa la frase matemática: "¿Cuánto es 10 + 1?" (Respuesta: 11), sino que se usa: "¿Cuánto es 1 más que 10?" (Respuesta: 11).
Nos cuenta de que con los cubos montables se presenta lo CONCRETO, que las imágenes del libro son lo PICTÓRICO y que las sumas realizadas según los algoritmos tradicionales son el abordaje ABSTRACTO o SIMBÓLICO. No aclara que las operaciones que nosotros llamamos "con canje" ó "con resto", se realizan con los bloques multibase y acá se llaman "con REAGRUPAMIENTO".
Desde la variabilidad perceptual, nos cuenta de que se aceptan diferentes estrategias para la búsqueda de resultados; que siempre se proyectan ejercicios que salen de lo tradicional para ayudar el proceso de análisis y creatividad en los alumnos y alumnas. Nos dice que la resolución de problemas es foco principal en el método y en este sentido siempre está abierto a la conexión de la matemática con la compresión lectora y la redacción o verbalización de expresiones matemáticas,
Nos muestra una actividad que según ella es ESTRELLA en el método Singapur y que es el estudio de los "Números Conectados": 10 = 8+2; 10 = 1+9 ; 10 = 4+6, etc., lo que nosotros conocemos como familias de números.
Nos muestra que el libro tiene partes anexas como: 1) el diario de Mates; 2) el calculo mental; 3) o problemas más complejos en la sección activa tu mente.
Fue dada por la educadora Daniela Goic, del colegio Pedro de Valdivia.
Daniela nos cuenta de que el Método Singapur se empezó a testear en colegios bilingues en el año 2009 -en Chile- y que su aplicación a le educación pública fue desde el año 2011. Ella lo practica desde el 2010.
Daniela nos aclara que la suya será un intervención no teórica sino más bien centrada en pequeñas prácticas que trae de su práctica cotidiana. Daiela nos muestra material concreto: pequeños cubos apilables o montables (de unidades para formar decenas); bloques de decenas (para formar centenas); bloques de centenas para formar unidades de mil; balanzas para adiciones, etc.
Nos habla de que en este método se usa la triada CO-PI-SI (COncreto - PIctórico - SImbolico ó Abstracto), heredada de Brunner, que realza el flujo desde lo enactivo a lo abstracto y que sin embargo tiene la abertura a que los chicos y chicas puedan comenzar en cualquiera de sus estadios o transitar libremente entre ellos.
Nos muestra que tras utilizar los pequeños cubos montables, para pasar de las unidades a las decenas, los chicos y chicas superan los ámbitos numéricos del MINEDUC rápidamente, por ejemplo donde se sugiere ir del 0 al 40, los niños y niñas alcanzan fácilmente del 0 al 100, lo que viene de la riqueza de trabajar con elementos concretos.
Nos dice que una de las grandes diferencias con la educación tradicional proviene de que -por la propia utilización de cubos montables- no se usa la frase matemática: "¿Cuánto es 10 + 1?" (Respuesta: 11), sino que se usa: "¿Cuánto es 1 más que 10?" (Respuesta: 11).
Nos cuenta de que con los cubos montables se presenta lo CONCRETO, que las imágenes del libro son lo PICTÓRICO y que las sumas realizadas según los algoritmos tradicionales son el abordaje ABSTRACTO o SIMBÓLICO. No aclara que las operaciones que nosotros llamamos "con canje" ó "con resto", se realizan con los bloques multibase y acá se llaman "con REAGRUPAMIENTO".
Desde la variabilidad perceptual, nos cuenta de que se aceptan diferentes estrategias para la búsqueda de resultados; que siempre se proyectan ejercicios que salen de lo tradicional para ayudar el proceso de análisis y creatividad en los alumnos y alumnas. Nos dice que la resolución de problemas es foco principal en el método y en este sentido siempre está abierto a la conexión de la matemática con la compresión lectora y la redacción o verbalización de expresiones matemáticas,
Nos muestra una actividad que según ella es ESTRELLA en el método Singapur y que es el estudio de los "Números Conectados": 10 = 8+2; 10 = 1+9 ; 10 = 4+6, etc., lo que nosotros conocemos como familias de números.
Nos muestra que el libro tiene partes anexas como: 1) el diario de Mates; 2) el calculo mental; 3) o problemas más complejos en la sección activa tu mente.
Etiquetas:
Charla,
La Escuela Aprende,
Método Singapur
jueves, 31 de diciembre de 2015
domingo, 27 de diciembre de 2015
Frase Matemática .....
"Los diseños del matemático, como los del pintor o los del poeta, tienen que ser hermosos; las ideas como los colores o las palabras, tienen que combinar de manera armoniosa. La belleza es la primera prueba: no hay un lugar permanente en el mundo para unas matemáticas feas."
G.H. Hardy
lunes, 21 de diciembre de 2015
Infinito en cómics
Suscribirse a:
Entradas (Atom)

























