lunes, 9 de noviembre de 2015
Será cierto?
sábado, 7 de noviembre de 2015
Proyecto POSTER CIENTIFICO - Matemático - Feria Ciencias 2015
|
1) Hacer un POSTER de buena
calidad Matemático-Científico: que anuncie la “Feria de Ciencias”. (Diciembre
11)
|
|
2) Saber EXPLICAR el POSTER
(al entregarlo).
|
|
3) Una selección de POSTERS
serán expuestos en la “Feria de Ciencias de la E.F.V. - 2015”.
|
viernes, 6 de noviembre de 2015
Así se hacen las mates en la EFV - Educadora Daniela Saldías
Math Rock (la idea de mirar esto es de Mauricio Garay, nuestro SABEDOR de música en la EFV)
Descripción
Grupos
Tomado de Youtube (Video)
jueves, 5 de noviembre de 2015
miércoles, 4 de noviembre de 2015
Genio

Ramanujan fue un genial matemático de principios del siglo XX. Nació en la India y allí apenas pudo estudiar porque no tenía libros. Sin casi formación matemática era capaz de intuir fórmulas que permitían encontrar resultados interesantísimos, como la que se ve en la imagen de arriba y que permite en cada iteración de la serie infinita obtener 8 decimales más del número pi.
Ramanujan envió cartas a varios matemáticos importantes del Reino Unido y casi nadie le dio importancia…excepto G. H. Hardy, que quedó impresionado por aquellas extrañas fórmulas que resultaban ser ciertas. Así que Hardy invitó a Ramanujan a trabajar con él en Reino Unido.
Allí, la salud del matemático indio, que siempre había sido delicada, empeoró. Cuentan que, estando Ramanujan ingresado en el hospital, recibió la visita de su amigo Hardy, que le dijo:
- He venido en un taxi con el número 1729, un número nada interesante.
Y Ramanujan le respondió:
- ¡No! ¡Es un número muy interesante! Es el número entero positivo más pequeño que puede expresarse como la suma de dos cubos de dos formas distintas.
En efecto: una forma es 1³+12³=1729, y la otra es 9³+10³=1729. Pero... ¿cómo se dio cuenta de eso Ramanujan así de repente? Cosas de genios. Desde entonces, al número 1729 se le conoce como "taxicab number".
lunes, 2 de noviembre de 2015
Euler
Euler
nació en Basilea en 1707, donde estudió junto con otro gran científico de la época, Johann Bernoulli. Con tan solo 23 años, fue nombrado catedrático de física, y tres años después de matemáticas. Euler fue un luchador innato, ya que antes de cumplir los treinta, comenzó a perder la vista de manera progresiva, hasta que se quedó casi ciego al final de su vida. Esto no le impidió ser una de las mentes privilegiadas de la investigación de la época, escribiendo numerosas obras científicas.Leonhard Euler realizó aportaciones muy diversas en campos como la aritmética, la física, la astronomía o la geografía. Gracias a su trabajo, hoy en días las cuestiones matemáticas y físicas se representan en términos aritméticos.
Su productividad fue enorme, hay quien considera que Euler escribía libros de altísima calidad científica de un tamaño de 800 páginas por año. Hoy dentro de su legado podemos encontrar una gran variedad de aportes a las matemáticas, tales como las fórmulas, los polinomios, las constantes o las líneas de Euler. También, cómo no, las integrales eulerianas, de gran impacto incluso hoy en día en la investigación. El doodle de hoy de Google también nos recuerda otro de los aspectos clave del trabajo de Euler: la introducción de la letra 'e' como base del logaritmo natural o neperiano.
Sus aportaciones científicas también fueron importantes en áreas como la teoría de grafos. En 1736, Euler fue capaz de resolver el conocido como "problema de los puentes de Königsberg". A la solución que aportó se le considera como el primer teorema de la teoría de grafos. Otros trabajos relacionados con la geometría incluyeron el teorema de los poliedros o el concepto conocido como característica Euler del espacio.
En conmemoración de su obra, Euler ha aparecido en la serie sexta de los billetes de 10 francos suizos, además de en sellos postales de Suiza y Alemania. Además de la celebración de Google de hoy, también fue reconocido al ser bautizado el "asteroide Euler" en su honor en 2002.
El infinito en un mazo de cartas ....
El infinito en un mazo de cartas
Fractales - Maravilloso !!!!
¿El próximo da Vinci? Un genio de las matemáticas usa fórmulas para crear arte .... (Tomado de Flipboard)
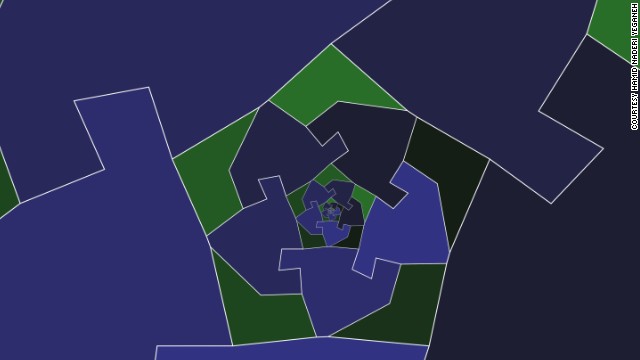
¿El próximo da Vinci? Un genio de las matemáticas usa fórmulas para crear arte.

Un pájaro de Yeganeh en vuelo fue creado a través de decenas de miles de imágenes generadas por ordenador. Este diagrama muestra la imagen en evolución, ya que diferentes valores numéricos se asignan a la fórmula.
Sucesos NO mutuamente excluyentes (Probabilidad Total) - 8avo. Medio
A) 15/90
B) 9/90
C) 21/90
D) 3/90
E) No se puede calcular.
Respuesta:
LLamemos a los sucesos:
Z : "ser divisible por 6"
Q: "ser divisiible por 10"
Construyamos los sucesos o eventos:
Z : "ser divisible por 6" = {6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90}
Q: "ser divisiible por 10" = {10, 20, 30, 40, 50, 60, 70, 80, 90}
Luego los sucesos Z y Q NO son mutuamente excuyentes, poseen intersección.
entonces la probabilidad pedida es:
Población y Muestra
Boole en Google ..... !!!!!
domingo, 1 de noviembre de 2015
Chiste probabilístico
Paul .... el loco de Paul ....
el mago de Budapest
Irune Gurrutxaga
Estimadas y estimados, una vez más, damos a conocer, o mejor dicho, recordamos a Paul Erdös, matemático que si bien era pequeño y escuchimizado, se hacía presente en infinidad de sitios, como luego veremos.
Erdös, que trabajó en infinidad de campos: teoría de grafos, de números, de conjuntos, de aproximación, combinatoria y probabilidad, análisis clásico, etc., pero que además se hizo célebre por su excéntrica personalidad, dejó memorables anécdotas entre los numerosísimos colegas con los que formó equipo a lo largo de su vida.
Paul Erdös nació en Budapest (Hungría) el 26 de marzo de 1913 en el seno de una familia de origen judío. Pocos días antes de su nacimiento, sus pequeñas hermanas de apenas 3 y 5 años morían de escarlatina, esa infecciosa enfermedad que aunque hoy día no tiene apenas incidencia en nuestra sociedad, en aquel tiempo era uno de los principales factores de mortalidad infantil. A este doloroso suceso, le acompañó el estallido de la Primera Guerra Mundial cuando Paul apenas acababa de cumplir un año. Su padre Lajos, que había sido movilizado para servir al ejército austrohúngaro, fue hecho prisionero por los rusos y llevado a Siberia y el pequeño Paul creció bajo cierta, y comprensible, sobreprotección por parte de su madre Anna. De hecho mantuvo a Paul alejado de la escuela hasta los 14 años y le proporcionó un tutor para que no tuviera que salir de casa. Parece que desde pequeño a Paul le apasionaban las matemáticas tanto como a sus padres, que eran profesores de esta materia.
Dicen que a la temprana edad de 3 años ya era capaz de sumar números de tres cifras con facilidad. Con estos antecedentes no es de extrañar que semejante niño prodigio fuera reconocido en su madurez como “el mago de Budapest” por la elegancia de sus métodos de resolución de problemas. La vida de Paul se desarrolló en un contexto histórico europeo muy complicado para todos, pero especialmente para los judíos. De hecho, recién terminada la Gran Guerra, por el Tratado de Trianon, Hungría fue desmembrada y perdió más del 70% de su territorio. El sentimiento de humillación y la mutilación territorial fue aprovechado por partidos ultranacionalistas que fueron asumiendo el control del país y promulgando unas leyes raciales antisemitas similares a las que trece años más tarde Hitler instauraría en Alemania.
A pesar de las restricciones a los judíos, Erdös, por su especial capacidad para las matemáticas, consiguió ingresar en la universidad de Budapest en 1930 y se doctoró con 21 años. A medida que se extendía el antisemitismo y el “sistema autocrático conservador” como definió a su gobierno el dictador Miklós Horthy, Paul, cumplidos 23 años, se trasladó a Manchester para realizar estudios de postgrado. En 1938, ante el clima prebélico que se respiraba en Europa, decidió establecerse en Estados Unidos, y fue en la Universidad de Princeton donde, en colaboración con Marc Kac, otro famoso matemático judío europeo exiliado, propuso su famosa “Teoría Probabilística de Números” llamada también Teorema de Erdös-Kac.
Al cabo de un año abandonó Princeton comenzando su extraordinario peregrinar profesional que le llevaría a recorrer numerosos países portando la vieja maleta con cuatro libros y una bolsa de plástico “de unos grandes almacenes de Budapest” como únicos enseres, que le caracterizaría a lo largo de su vida. Y es que, como le gustaba decir, todo lo importante lo llevaba en su cabeza. Se dedicaría en adelante a recorrer el mundo, de universidad en universidad, de casa en casa, llevando una vida nada convencional, sin buscar honores ni premios y sin importarle nada más que las matemáticas.
Tampoco los convencionalismos sociales porque tenía la “manía” de presentarse sin previo aviso, sin importarle ni la hora ni el día, con la frase “abre tu mente porque vengo a traerte la luz”. Este deambular no impidió a Erdös publicar más de 1500 artículos, la mayoría en coautoría, en toda clase de revistas y desde todas las partes del mundo, tanto es así que se llegó a decir que aquel que no hubiera tenido el honor de recibir la visita de Erdös no era un verdadero matemático. Y es que nuestro peculiar personaje no estaba hecho para las formalidades ni normas. Paul Erdös falleció el 20 de septiembre de 1996 a la edad de 83 años, mientras asistía a una conferencia en Varsovia (Polonia). De un fallo del corazón, se dijo. Pero como veremos más adelante a Erdös si algo no le falló, en vida, además de su mente, era su buen corazón. En el bolsillo de su chaqueta llevaba la documentación que le acreditaba para su próxima conferencia en Lituania. Se puede afirmar que Erdös murió como vivió, viajando de un país a otro.
Tras su muerte, la comunidad matemática estableció una curiosa numeración llamada “número de Erdös”. Mediante este número se establecía la influencia de un matemático en la comunidad científica. Paul Erdös tenía fijado, como no podía ser de otro modo, el número de Erdös igual a 0. Cualquier persona que hubiera colaborado con él tendría asignado el número de Erdös igual a 1. Toda persona que hubiera trabajado con una persona que tuviera número de Erdös igual a 1 tendría asignado el número de Erdös igual a 2 y así sucesivamente. Figura 2: El número de Erdös. ¿Pero por qué se estableció este curioso número de Erdös? Puede entenderse si decimos que hay constancia de que Erdös colaboró con más de 600 matemáticos y matemáticas de todas partes del mundo. Se comenta que en los selectos y exclusivos círculos matemáticos es muy difícil encontrar a un matemático o matemática que tenga un número de Erdös mayor a 8, precisamente por la cantidad de colaboraciones y publicaciones que hizo nuestro singular personaje.
Por otro lado, tal fue la resonancia vital de Erdös que, en la St. Gregory’s of Nysses, una iglesia episcopaliana de San Francisco, encontramos en un mural del ábside a Paul “bailando” nada menos que entre Ghandi y Martín Lutero; y es que en esta extraordinaria iglesia se representa una procesión de 90 “santos danzantes” de diferentes religiones y distintas disciplinas. Ahí encontramos todo tipo de personas que han aportado su conocimiento, inspiración o arte en campos como la música, el cine, el deporte, la ciencia, la arquitectura, la religión, el pensamiento, etc. Para los fieles de esta congregación estos “santos y santas” han sido bendecidos por el toque divino que les ha hecho destacar en su especialidad, sin importar raza, sexo ni religión y por ello se merecen un hueco en esta
iglesia. Y ahí merece estar Erdös
.El “santo” Erdös danzando. Para terminar esta aproximación a Paul Erdös, procede relatar alguna de las anécdotas de la faceta “friki” de su carácter y personalidad que no dejaba a nadie indiferente. Erdös, nacido judío, decía de si mismo que era ateo y se refería a Dios como el Supremo Fascista que se guardaba las demostraciones más hermosas sin compartirlas con los humanos. En contraposición a la Torah, a la Biblia o al Corán, “Libros” donde se recogen las revelaciones divinas, para Erdös El Libro verdadero, no era ninguno de aquellos, sino un libro imaginario en el cual Dios tenía escritas esas hermosas pruebas de los teoremas matemáticos y que serían adquiribles solo por el esfuerzo y la capacidad de razonamiento científico.
Erdös también fue conocido por su humildad y por su compasión, una prueba de ello es que cuando recibió en 1984 el prestigioso premio Wolf en Matemáticas, de los 50 000$ que recibió, solo se quedó con 720$. Vaya uno a saber por qué se quedó exactamente con esa cantidad pero era habitual en Erdös, que casi todo el dinero que ganaba lo dedicara, además de ayudar económicamente a personas más necesitadas, a los premios que el mismo otorgaba y que iban de 10$ por la resolución elegante de un problema sencillo, hasta los 10.000$ por un problema “sin esperanza” como él solía llamarlos. Y es que este bohemio de la ciencia, que no tuvo ni mujer ni descendencia, sólo necesitaba el capital estrictamente necesario para proseguir su deambular y particular viaje. ¡Ah! y su vieja maleta con cuatro libros y su bolsa de plástico casera. Todo lo demás lo llevaba consigo siempre. En su cabeza.