martes, 31 de marzo de 2015
lunes, 30 de marzo de 2015
3 ejercicios de Raíces - 2do. Medio (Ejercicio Resuelto)
Problema 1) Alternativa B)
Problema 2) Alternativa B)
Problema 3) Alternativa C)
miércoles, 25 de marzo de 2015
Autocrítica del Taller de Mates en el Primer Ciclo Básico
Un primer pasito de este proyecto transversal de matemáticas "las matemáticas al patio" partió la recién pasada última semana de Marzo. Como las grandes y los grandes de la ciencia, chicas y chicos jugaron a buscar regularidades en la naturaleza. Dejaron caer bolitas de cristal en una tablas de Galton, para intentar descubrir la formación de la campana de Gaus. La pregunta quedó instalada y en primera intancia -estos peques científicas y científicos de 1ro. y 2do básico- graficaron los datos en un pictograma. Tabién hacemos matemáticas y ciencias en la Escuela Francisco Varela.
Bondades:
Bondades:
=========
1) Nos atrevimos.
2) Nos preparamos, preparamos materiales diligentemente: nariz, gorro, lente, mesa, lugar, hoja de contestar, quincunce, estudiamos el quincunce o tabla de Galton, lo compartimos entre los tres, etc.
3) Concitamos atención: cuajó el deseo de participar, aunque eso se debe a los niños y niñas en gran parte, que son amorosos y amorosas!
Cuestiones menos buenas:
=======================
1) Es corto el tiempo. La actividad muy larga, agotadora.
2) NO calibramos bien la metáfora con la edad.
3) No pensamos escenarios favorables y menos favorables: No pensamos en alguien, que por ejemplo, le diera penita.
4) No usamos elementos que nos permitieran dosificar la participación.
5) No conversamos bien con los que hacen mates en los niveles abordados, al punto que allí supimos las habilidades no tenidas y que nosotros usábamos.
6) No registramos!
7) No planificamos la incursión de la clown ....
¿Qué piensan Uds.?
lunes, 23 de marzo de 2015
El poder de un Beso (x Marta Macho Stadler)
El poder de un beso es una de las obras de la artista Minjeong An (1981-), creación que obedece la segunda ley de Newton F = ma, donde:
- F (fuerza): del beso (medida en N)
- m (masa): 23 kg x saliva de la madre
- a (aceleración): kF/m, donde ‘k’ es un factor de proporcionalidad = amor de madre (constante)
Minjeong An mide longitudes, distancias, ángulos… todo se transfiere al papel, incluso lo invisible a nuestros ojos se representa mediante símbolos.
Y después, la física entra en juego…
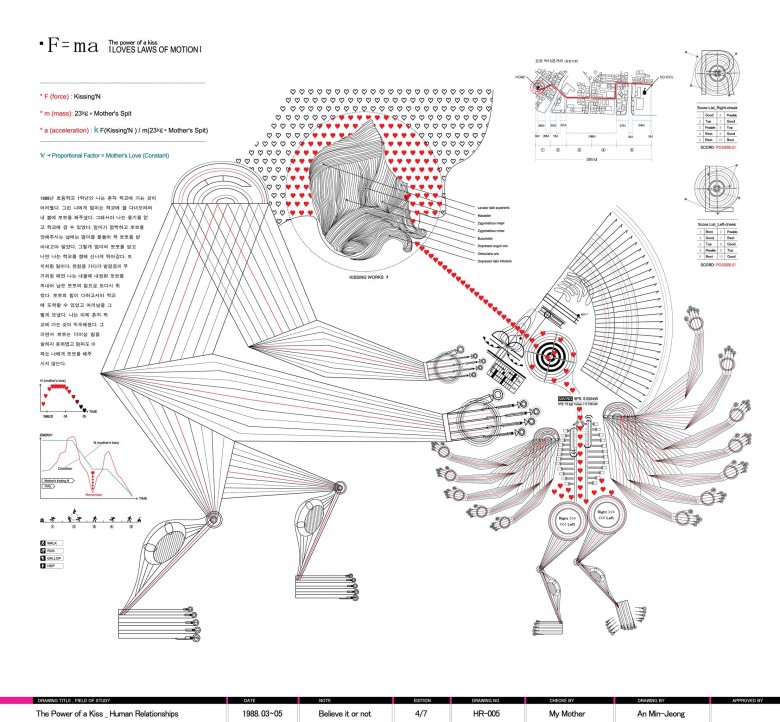
Cuando yo era una estudiante de la escuela primaria en 1989, era difícil para mi ir a la escuela sola. Sin embargo, mi madre me daba un beso cuando me enviaba a la escuela, entonces, me animaba a ir. […] Cuando estaba cansada de caminar hacia la escuela, me recargaba el poder del beso de mamá guardado en mi cara. Llegaba a la escuela después de que el poder de su beso se agotara. […]
Minjeong An
Recuadro 1: Fuerza = masa x aceleración
Recuadro 2: el poder y el efecto del beso
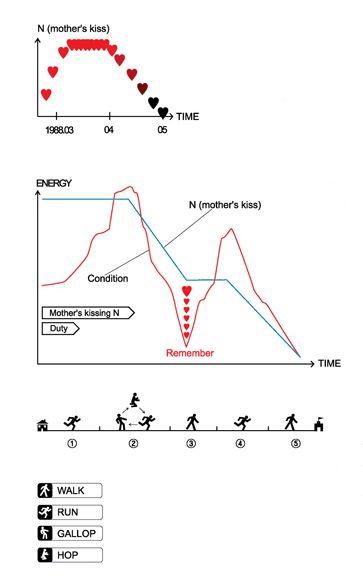
Recuadro 3: el recorrido de la casa al colegio
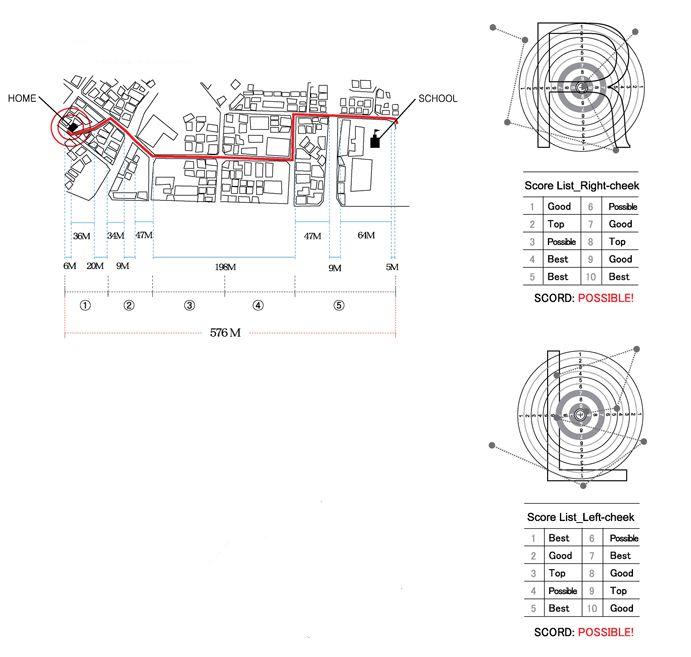
Recuadro 4: el beso se lanza
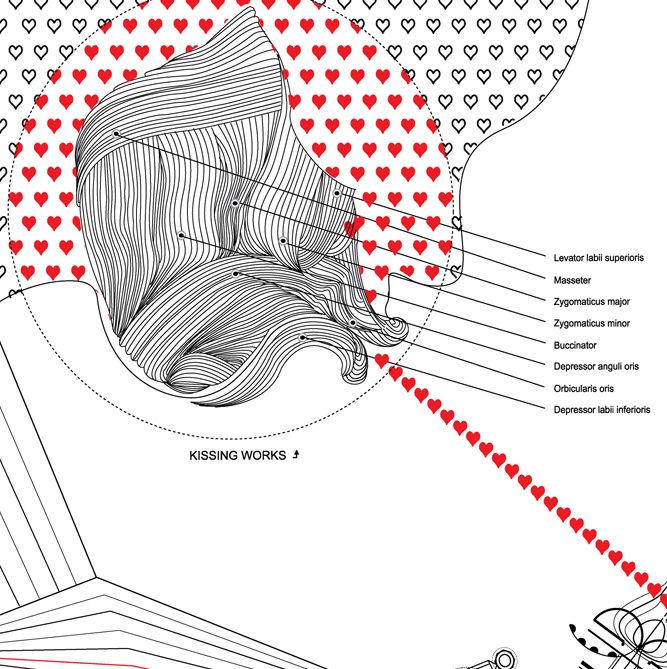
Recuadro 5: los efectos del beso
Una bonita manera de celebrar el Día Mundial de la Poesía.
No dejéis de vistar la página de Minjeong An, sus ilustraciones tienen mucho arte… y mucha ciencia.
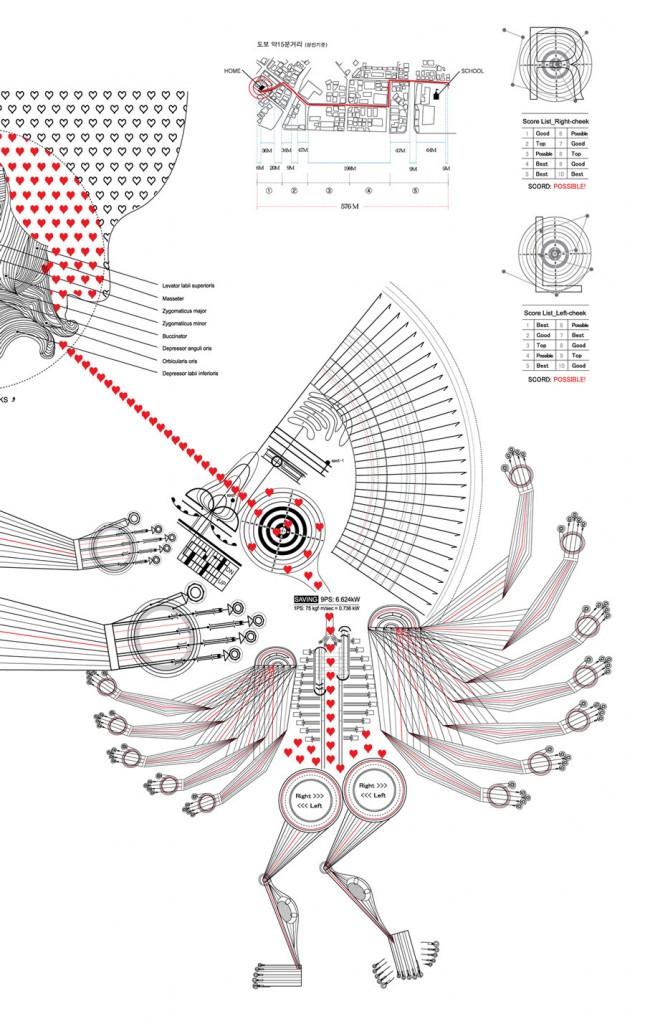
Más información
- Marta Macho Stadler, El poder de un beso: F = ma, ::ZTFNews, 2014
- Minjeong An – ilustración digital, Forma es vacío, vacío es forma, 2013
- Arte con diagramas, por Minjeong An, Choosa, 2012
El AGUA ....
Día Mundial del Agua 2015: «Agua y Desarrollo Sostenible»
Published 22/03/2015 Aut.: M. Macho , Biología , Ecología , Eventos , Medio Ambiente ,Responsabilidad social , Salud Leave a CommentEtiquetas: Día Mundial del Agua, Día Mundial del Agua 2015: «Agua y Desarrollo Sostenible»,Decenio Internacional para la Acción «El agua fuente de vida» 2005-2015, desarrollo sostenible,World Water Day
Para eliminar los múltiples problemas relacionados con el agua, debemos trabajar con un espíritu de cooperación urgente, con mente abierta a las nuevas ideas y la innovación, y dispuestos a compartir las soluciones que todos necesitamos para un futuro sostenible.
Mensaje del Secretario General Ban Ki-moon en el Día Mundial del Agua, 22 de marzo de 2015
- El agua es salud: Lavarte las manos puede salvar tu vida
- El agua es naturaleza: Los ecosistemas están en el corazón del ciclo global del agua
- El agua es urbanización: Cada semana, un millón de personas se traslada a las ciudades
- El agua es industria: Se utiliza más agua en la fabricación de un coche que en llenar una piscina
- El agua es energía: El agua y la energía son amigos inseparables
- El agua es comida: Para producir dos filetes se necesitan 15.000 litros de agua
- El agua es igualdad: Cada día las mujeres invierten millones de horas transportando agua
El agua es… salud, naturaleza, urbanización, industria, energía, comida, IGUALDAD
Más información:
- Galería de fotos
- Día Mundial del Agua de 2015
- Decenio Internacional para la Acción «El agua, fuente de vida» 2005-2015
- World Water Day
- Póster: A day for water and water for SUSTAINABLE DEVELOPMENT
- Todos los pósteres
¿Por qué la Andrea se sabe las Tablas?
Departamento de Matemáticas Escuela Francisco Varela
¿Por qué la Andrea sabe las Tablas?
RECURSOS Waldorf para el Aula.
==========================
por Claudio Escobar Cáceres,
una mirada personal de las ideas Waldorf ....
================================
Más allá del recurso publicitario sugerido en la pregunta que encabeza de este artículo (¿Por qué la Andrea sabe las Tablas?), la intención primordial es, construir poco a poco un "Hilo de Ariadna", para que nosotros(as) Teseos, podamos ingresar al laberinto de las matemáticas.
Pero, ....
¿por qué este lenguaje mítico/arquetípico para comenzar esta conversa?
La metodología Waldorf para la enseñanza de las matemáticas no está focalizada exclusivamente en el pensamiento racional, busca promover lo inconsciente, las intuiciones, ciertas imágenes que se corresponden con elementos míticos o imágenes primordiales.
Las matemáticas Waldorf parten de un mundo animado, en el estilo de Morris Bergman y su re-encantamiento del mundo, en el sentido de que el universo entero está preñado de animus, de elementos matemáticos que se encuentran como PRE-FORMA en las imágenes primordiales intuitivas.
La inteligencia sería provocar las matemáticas desde allí. La mirada Waldorf explora y busca activar, modelos que habitan como huellas en el insconsciente.
Cuando Andrea al presentar por primera vez los números -en primero básico- dice:
"YO SOY .... la unidad y en mí están todos los números"
Está invocando el sentido de la unidad como factor fundante, está evocando que la unidad es el todo que contiene a los elementos, está conspirando con una unidad-universo-contenedora: que lo contiene todo, o quizás ....
está evocando, urgando -directamente- en la línea del mito del dios egipcio Atom ....
Atom representa el gran UNO indivisible de la Enéada egipcia o los nueve dioses, que son las partes de esta deidad llamada Atom. Las 9 deidades reunidas representan al demiurgo Atom, quien dará origen a la vida. Atom es un dios eterno, abarcador, invisible. Atóm es la unidad que contiene al todo y en sintonía con una serie de imágenes míticas de otras culturas, está evocando el principio de la unicidad contenedora.
Este y otros mitos han surcado huellas en la memoria colectiva del insconciente, huellas mnémicas o arquetípicas, que quedaron arquitecturadas para siempre dentro de la psiquis del ser humano.
Cuando los chicos entienden/sienten la imagen externa del gesto que provoca el "Yo soy la unidad y en mi están todos los números" - tras lo cual presenta el dos (2): las manos; el tres (3): las partes del cuerpo, el cuatro (4): los elementos en el rostro, etc., se produce una especie de ensamblaje de lo observado exteriormente con imágenes anteriores, primordiales de la especie humana.
Pero atención, las y los maestros Waldorf nos invitan en un inicio, a no conceptualizar más allá. Por ejemplo, tras hacer el juego de saltar con las tablas nos piden que en un inicio no digamos de inmediato: esta es la tabla del 2! .... PRIMERO: Jugar! .... porque hay saberes al menos en un comienzo inconceptualizables, quizás metaforizables, que deben partir generando internamente, lejanos de las imágenes demasiado o apresuradamente simbólicas.
Estas imágenes iniciales se abren en la bifurcación: LOGOS-MITO, por el sendero de lo mítico, son más bien NO-racionales y se enseñorean en un tiempo primordial, sagrado, cualitativo y eterno .... se alejan del tiempo profano, exacto y cronológico de la ciencia: son juegos sin tiempo, sin logos. Lo otro vendrá después ....
¿Y qué pasa con las tablas?
====================
LINK: Herramienta Tablas de Multiplicar - Waldorf
Volvamos a los ciclos de la naturaleza: Está en la esencia del ser humano el entendimiento de los sucesos significativos del cielo: Cielo y Tierra comparten un devenir cíclico, este entendimiento nos lleva a lograr confianza futura y lucidez: mañana volverá a salir el sol .... y por la noche, nuevamente la luna.
Es por esto que las tablas en urdimbre cíclica se fijan más fáciles, porque:
1) Evocan el círculo, el círculo humano (Trawum), el fuego y sus beneficios.
2) Provocan inconscientemente -en un proceso- el descubrimiento de patrones.
3) Exponen estos patrones a interrelaciones mayores, en el proceso hacia lo simbólico.
4) Nos hacen recorrer nuevamente una huella que se ha arquitecturado en la conciencia colectiva.
Este tipo de camino es un círculo virtuoso para la posterior creación de un mapa simbólico, abstracto.
Lo que en definitiva trato de decir, es que en imágenes míticas, en cuentos llenos de alma: elementos de la "matedología" Waldorf, hay gestos arquetípicos tradicionales. Una mente que explora en matemáticas, ayudada de cuentos e imágenes míticas, está volviendo a recorrer una huella que se instaló otrora .... los chicos y chicas sienten haber descubierto o inventado pequeñas reglas matemáticas, cuando lo que sucede es que se reactivan imágenes primordiales pre-forma y esto es, realmente es un buen camino ....
Pero hay otras miradas complementarias .... !!!!
Para finalizar, activo un Power Point que fue resultado de conversaciones en el departamento de Matemáticas, en el año 2014, Provecho!
en la línea de lo anterior,
Narrando Historias en Matemáticas:
Narrando historias en matemáticas from Claudio Escobar
LINK: Tabla del 3 con Herramienta Waldorf: Tabla 3 Herramienta Waldorf
LINK: Tabla del 3 con Herramienta Waldorf: Tabla 3 Herramienta Waldorf
viernes, 20 de marzo de 2015
maravilloso !!!!!
... el asunto no es que sea una idea loca,
el asunto es si es suficientemente loca.
Niels Bohr.
Tarea - Ejercicios Combinados en Z - Paréntesis - Protocolos de Operación
Por si alguien perdió la guía .... siempre cuenten conmigo, Clau
Guía 8avo - Tarea Fin de Semana 21 y 22 de Marzo
Un ejemplo:
Resolver:
80:[25-3+(-2)1] - 32
Al interior del paréntesis, resolvemos, antes de sumar, la multiplicación:
80:[25 - 3 -2] - 32
Luego sumamos al interior, de IZQUIERDA a DERECHA
(¿es esto, aquí, obligatorio? * )
80:[22 - 2] - 32
Resolvemos el paréntesis
80:20 - 32
Antes que la suma (o resta), resolvemos la división:
4 - 32
+4 + -32
-28
Respuesta: ( * )
Cuando se suman y restan cantidades como: 25 - 3 - 2
en las cuales se distinguen en forma clara los positivos de los negativos,
no es necesario ir encadenadamente de izquierda a derecha.
Mucha gente junta los positivos, junta los negativos y opera estas dos cantidades finales:
25 - 3 - 2
25 - 5
20
(llegamos al mismo resultado)
¿Entonces, cuándo se opera de izquierda a derecha?
Cuando hay situaciones con combinación de signos:
30 -(-28) + 8
Acá el error sería operar -28 + 8 = -20
y luego:
30 -(-28) + 20
30 -(-20)
30 + 20
50 (Esto es error)
Se opera de dos formas posibles:
Primera alternativa:
30 -(-28) + 8 (Convirtiendo resta a suma)
30 + +28 + 8
66
Segunda Alternativa:
30 -(-28) + 8 (multiplicando los signos menos
30 + 28 + 8
66
Guía 8avo - Tarea Fin de Semana 21 y 22 de Marzo
Un ejemplo:
Resolver:
80:[25-3+(-2)1] - 32
Al interior del paréntesis, resolvemos, antes de sumar, la multiplicación:
80:[25 - 3 -2] - 32
Luego sumamos al interior, de IZQUIERDA a DERECHA
(¿es esto, aquí, obligatorio? * )
80:[22 - 2] - 32
Resolvemos el paréntesis
80:20 - 32
Antes que la suma (o resta), resolvemos la división:
4 - 32
+4 + -32
-28
Respuesta: ( * )
Cuando se suman y restan cantidades como: 25 - 3 - 2
en las cuales se distinguen en forma clara los positivos de los negativos,
no es necesario ir encadenadamente de izquierda a derecha.
Mucha gente junta los positivos, junta los negativos y opera estas dos cantidades finales:
25 - 3 - 2
25 - 5
20
(llegamos al mismo resultado)
¿Entonces, cuándo se opera de izquierda a derecha?
Cuando hay situaciones con combinación de signos:
30 -(-28) + 8
Acá el error sería operar -28 + 8 = -20
y luego:
30 -(-28) + 20
30 -(-20)
30 + 20
50 (Esto es error)
Se opera de dos formas posibles:
Primera alternativa:
30 -(-28) + 8 (Convirtiendo resta a suma)
30 + +28 + 8
66
Segunda Alternativa:
30 -(-28) + 8 (multiplicando los signos menos
30 + 28 + 8
66
jueves, 19 de marzo de 2015
Espiral de Teodoro de Cirene
Posee un error, las figuras planas que ayudan a lograr los irracionales DEBEN ser triángulos rectángulos ....
miércoles, 18 de marzo de 2015
martes, 17 de marzo de 2015
A los 4 añitos ....
Los niños de cuatro años ya tienen nociones de geometría euclidiana
Un estudio liderado por investigadores de la Universidad de Harvard (EEUU) ha revelado que los niños de cuatro años poseen habilidades que podrían representar una comprensión temprana de la geometría euclidiana. El trabajo ha analizado en niños la relación entre su sentido de la orientación, su capacidad de analizar formas y su interpretación de mapas simbólicos.
Los adultos humanos de diferentes culturas comparten intuiciones sobre puntos, líneas y figuras de la geometría euclidiana. Ya desde niños desarrollan nociones tempranas para orientarse en el espacio y analizar la forma de los objetos, pero ¿cómo llegan al pensamiento euclidiano?
Según un estudio que se presenta esta semana en la revista Proceedings of the National Academy of Sciences (PNAS), a los cuatro años de edad los humanos ya poseen habilidades que demuestran una comprensión temprana de la geometría euclidiana.
El trabajo, liderado por investigadores de la Universidad de Harvard, ha estudiado en niños la relación entre su sentido de la orientación, su capacidad de analizar formas y su interpretación de mapas simbólicos.
Según el artículo, muchos animales, incluidos los humanos, poseen un entendimiento innato de la geometría simple. Reconocen objetos mediante ángulos y longitudes relativas, y se desplazan por su entorno empleando nociones de distancias y direcciones. Unidas, estas dos representaciones geométricas básicas podrían formar la base del pensamiento abstracto geométrico exclusivo de los humanos.
Según este nuevo trabajo, los niños no parecen integrar tales nociones; sin embargo, sí hacen un uso flexible de la geometría abstracta en la lectura de mapas, lo que podría llevar a la posterior construcción de la geometría euclidiana.
Uno de los experimentos llevados a cabo en el estudio consistió en vendar los ojos de los niños participantes y hacer que giraran para ver cómo se orientaban, tras destaparles los ojos, en un área con forma rectangular. También se les hizo pasar un test de ordenador que evaluaba su habilidad para reconocer distintas formas geométricas.
Como animales en su hábitat
Después se situó a los niños en el centro de dos áreas con forma de triángulo. En uno de los dos escenarios del experimento, el triángulo tenía sus tres lados pero le faltaban todas las esquinas. En el otro, le faltaban los lados y solo tenía las tres esquinas. Los investigadores mostraron a todos los niños los mismos mapas para que localizaran ciertos puntos en el borde del triángulo donde debían colocar un juguete de peluche.
Moira Dillon, coautora del estudio, explica que los niños que mejor manejaban distancias y direcciones ubicaron bien el peluche en el triangulo sin esquinas. En cambio, los más hábiles en las pruebas de reconocimiento de formas geométricas en el ordenador obtuvieron resultados superiores en el triángulo compuesto solo por esquinas.
El trabajo sugiere que las habilidades geométricas tempranas son las mismas que las que usan los animales para moverse en su hábitat. Según los investigadores, en torno a los dos años y medio, los niños empiezan a ser capaces de abstraer esos principios para leer mapas adaptando a cada situación el tipo de información que emplean, como en el caso de los dos escenarios triangulares.
Referencia bibliográfica:
Moira R. Dillon, Yi Huang, Elizabeth S. Spelke. "Core foundations of abstract geometry”. Proceedings of the National Academy of Sciences (PNAS), 12 de agosto de 2013.
lunes, 16 de marzo de 2015
domingo, 15 de marzo de 2015
10 puntos para entender los números Reales ( IR ) - 2do. Medio - Escuela Francisco Varela
INFINITOS por todas partes ....
por Claudio Escobar Cáceres
Departamento de Matemáticas
Escuela Francisco Varela
0)
Los matemáticos distinguen varios tipos de números, con propiedades diferentes. Lo que realmente importa no son los números individuales, sino el sistema al que pertenecen: la compañía en la que están.
Algunos de estos sistemas o conjuntos numéricos son:
IN: Naturales.
Los números de contar, esos que "vemos en la naturaleza"
IN = {1,2,3,4,5,.....}
Son infinitos, tienen un primer número, pero no un final.
- - - - - - - - - -
INo: Cardinales.
Son los Naturales agregados del cero.
INo = {0,1,2,3,4,5, .....}
Son también infinitos, tienen un primer número, pero tampoco un final.
Este conjunto numérico, contiene al anterior.
- - - - - - - - - -
Z: Enteros.
Son los naturales, más los naturales con signo negativo, más el cero.
Z = { .... -5, -4, -3, -2, -1, 0, 1, 2, 3, .... }
Son infinitos, no tienen principio ni fin.
Z contiene a IN, Z contiene a INo
- - - - - - - - - -
Q: Racionales.
(acá hay fracciones y decimales, aunque NO todos los decimales, porque algunos decimales son de otro tipo: Irracionales)
Q contiene todas las fracciones, positivas y negativas. También contiene a todos los enteros, porque cada entero se puede poner como fracción, simplemente dividiendo por 1.
Q = { .... -5, -9/2, -4, -3, -2, -3/2, -1, -1/3, 0, 1, 2/3, 2, 3, 4, 5, 11/2, .... }
Nuevamente Q contiene a Z, Q contiene a INo, Q contiene a IN.
Hasta acá conocemos, por lo general, hasta 1ro. medio.
Pero aparece otro Conjunto, los Irracionales .... Los irracionales NO contienen a ninguno de los anteriores conjuntos ....
Los racionales unidos a los irracionales conforman un conjunto mayor llamado Los Reales.
Veamos esto en un esquema:
Pero OJO Piojo:
============
IR contiene a Q
IR contiene a Q*
IR contiene a Z
IR contiene a INo
IR contiene a IN
Q* NO contiene a ninguno de los otros Conjuntos Numéricos!
Y como diagramas de Venn, pero en Brasileiro, ja ja ja !!!!
1)
Los números Reales ( IR ), están formados por la unión de dos conjuntos: Los Racionales ( Q ) y los Irracionales ( Q* ).
es decir,
Q: Racionales:
Son aquellos que se pueden escribir como fracción. Incluye a los decimales finitos, los periódicos y los semiperiódicos.
ejemplos:
2,3 (Finito) ;
-3,185 (Otro Finito) ;
0,33333..... (Periódico) ;
-5/8 ;
0,6666.....(Otro periódico) ;
-1/3 ;
2,7891212121212.... (Semiperiódico) ....
Q*: Irracionales:
Son aquellos que NO se pueden escribir como fracción, poseen un desarrollo decimal infinito en el cuál jamás se repite algún tipo de período.
ejemplos:
Al conjunto de los Reales se le conoce también como "El Continuo" ....
Nota:
Toda fracción puede escribirse como decimal, PERO
NO TODO decimal puede escribirse como fracción.
2)
Los números Reales, dijimos, se forman por la unión de los Racionales (Q) y los Irracionales (Q*).
La sola presencia de los Racionales (Q), deja incompleta la Recta Numérica, es decir, si en una recta numérica graficamos Q, que contiene como subconjuntos a IN, INo y Z, la recta estaría llena de hoyos o agujeros .... faltarían infinitos números: Faltarían los Irracionales !!!!
3)
Hasta IN, INo, Z y Q, los conjuntos numéricos se llaman ENUMERABLES, porque se pueden hacer corresponder biunívocamente (uno a uno) con los números Naturales (IN) o de contar.
De allí en adelante, es decir, Tanto los Irracionales (Q*), como los Reales ( IR), hablamos de Conjuntos Numéricos NO Enumerables, porque no se pueden hacer corresponder biunívocamente con los Naturales ( IN ).
Esto lo descubrió o al menos lo demostró Cantor.
4)
George Cantor (1845 - 1918): Matemático alemán, de origen ruso, creador de la Teoría Axiomática de Conjuntos, y el primero capaz de expresar formalmente en lenguaje matemático la idea o noción de INFINITO, bajo la forma de un nuevo conjunto numérico, los números Transfinitos.
Las ideas de Cantor acerca del infinito recibieron una crítica generalizada que tal vez agravó su tendencia crónica a la depresión, lo que a su vez le llevó muchas veces a estar internado. Sin embargo su obra se hizo trascendente y fundamental para las matemáticas actuales.
El matemático David Hilbert describió el trabajo de Cantor como "el producto más depurado de genio matemático y uno de los mayores logros de la actividad intelectual pura".
5)
Los números Racionales (Q) son infinitos y también lo son los Reales (R); sin embargo, hay más números Reales que Racionales. Georg Cantor, matemático del siglo XIX, fue el pionero en investigar esta aparente paradoja, remeciendo las bases de la matemática que se conocía al momento: al afirmar que existen distintos tipos de infinitos: algunos mayores que otros.
6)
Entre los años 1870 y 1880 Cantor y Dedekind iban a operar un cambio REVOLUCIONARIO.
De aquello que se había siempre pensado una imposibilidad: que la parte sea igual al todo, ellos hicieron una propiedad.
Ellos mostraron utilizando la correspondencia biunívoca, que el conjunto de los naturales ( IN: Números de contar ) es tan grande como los pares, por ejemplo, porque se puede hacer una correspondencia biunívoca entre los Naturales y los Pares (o impares).
El Conjunto de los Naturales ya no es mayor que el conjunto de los Pares, o de los Impares.
A este conjunto enumerado (hecho corresponder numéricamente con los naturales) se le llama Infinito Numerable o Enumerable o a veces Infinito Discreto.
De igual forma demostró Cantor que hay tabtos Naturales como Enteros (Z) y Racionales (Q).
En la imagen, una intervención artística personal a la obra de Max Ernst.
7)
¿Es el numerable el único infinito?
Cantor responde que NO.
La potencia de los números Reales es mayor que el numerable.
En efecto es imposible construir una correspondencia biunívoca entre IN y R.
Es decir, hay infinitamente más puntos en la Recta Numérica que números Naturales (o Cardinales o Enteros, o Racionales).
Tenemos dos Infinitos:
1) El numerable ( IN; INo; Z; Q)
2) el de IR, denominado "El Continuo".
Pero cuidado, de nuevo, por más asombro que le cause: No hay más puntos en todo IR, que en el segmento [0,1].
8)
Cantor dice que SÍ, que hay otros infinitos más grandes .... Dice que el conjunto de las partes de un conjunto A, tiene una potencia superior.
El conjunto de todos los subconjunto de IR, posee una INFINITUD MAYOR ....
Podemos partir de IN, luego seguir con Z, Q, Q* y construir sus conjuntos de subconjuntos ....
Hay una infinidad de infinitos.
9)
Dos tipos de Infinitos:
Así:
IN: Naturales: Alfa Cero (Infinito Numerable)
INo: Cardinales: Alfa Cero (Infinito Numerable)
Z: Enteros: Alfa Cero (Infinito Numerable)
Q: Racionales: Alfa Cero (Infinito Numerable)
------------------------------------------------------------
Q*: Irracionales: Alfa 1 (Infinito No Numerable)
IR: Reales: Alfa 1 (Infinito No Numerable)
10)
El infinito que a mi me gusta ....
Katsushika Hokusai, uno de los artistas japoneses más conocidos a nivel mundial, realizó cerca de treinta mil obras de arte a lo largo de su carrera. Aunque su estilo dista mucho del arte tradicional japonés, su obra es clave en las historia de la producción artística de este país.
Hokusai nació en 1760, en el seno de una familia de artesanos en la provincia japonesa de Edo. Comenzó a pintar desde que tenía seis años, muy probablemente bajo la tutela de su padre, cuyo trabajo era hacer espejos y decorar los marcos con meticulosas ornamentas. En 1779 publicó sus primeras piezas de ukiyo-e –estampas japonesas que mostraban distintas costumbres– como parte de una serie de impresos sobre teatro Kabuki. Durante su primera etapa creativa su estilo se regía por la tradición japonesa, tanto en técnica como en temática, pero a finales del siglo XVIII adquirió varios grabados calcográficos en cobre hechos en Francia y Holanda, que lo llevaron a explorar con diferentes estilos de Occidente. Esto influyó en los temas que trataba en sus obras, se alejó de los actores Kabuki y los cortesanos para enfocarse en el paisaje y en imágenes cotidianas de la vida en Japón, un cambio fundamental tanto para el artistas como para el género ukiyo-e.
La obra más famosa de Hokusai es Treinta y seis vistas del Monte Fuji, una serie de 36 xilografías realizadas entre 1831 y 1833. En una segunda publicación se añadieron diez xilografías más a la serie en las que el artista japonés retrata al Monte Fuji desde diferentes perspectivas y en distintas condiciones climáticas.
La gran ola de Kanagawa, también conocida como La gran ola, es la pieza más reconocida de la serie y de la carrera de Hokusai. De ésta se realizaron miles de copias, y varias llegaron a manos de coleccionistas europeos. A partir de la década de 1870, La gran ola se volvió muy popular entre artistas y coleccionistas franceses.
por Claudio Escobar Cáceres
Departamento de Matemáticas
Escuela Francisco Varela
en construcción .....
"Dios creó los números,
el resto es obra del ser humano"
(Leopold Kronecker)
0)
Los matemáticos distinguen varios tipos de números, con propiedades diferentes. Lo que realmente importa no son los números individuales, sino el sistema al que pertenecen: la compañía en la que están.
Algunos de estos sistemas o conjuntos numéricos son:
IN: Naturales.
Los números de contar, esos que "vemos en la naturaleza"
IN = {1,2,3,4,5,.....}
Son infinitos, tienen un primer número, pero no un final.
- - - - - - - - - -
INo: Cardinales.
Son los Naturales agregados del cero.
INo = {0,1,2,3,4,5, .....}
Son también infinitos, tienen un primer número, pero tampoco un final.
Este conjunto numérico, contiene al anterior.
- - - - - - - - - -
Z: Enteros.
Son los naturales, más los naturales con signo negativo, más el cero.
Z = { .... -5, -4, -3, -2, -1, 0, 1, 2, 3, .... }
Son infinitos, no tienen principio ni fin.
Z contiene a IN, Z contiene a INo
- - - - - - - - - -
Q: Racionales.
(acá hay fracciones y decimales, aunque NO todos los decimales, porque algunos decimales son de otro tipo: Irracionales)
Q contiene todas las fracciones, positivas y negativas. También contiene a todos los enteros, porque cada entero se puede poner como fracción, simplemente dividiendo por 1.
0 = 0/1
7 = 7/1
-893 = -893/1
Q = { .... -5, -9/2, -4, -3, -2, -3/2, -1, -1/3, 0, 1, 2/3, 2, 3, 4, 5, 11/2, .... }
Nuevamente Q contiene a Z, Q contiene a INo, Q contiene a IN.
Hasta acá conocemos, por lo general, hasta 1ro. medio.
Pero aparece otro Conjunto, los Irracionales .... Los irracionales NO contienen a ninguno de los anteriores conjuntos ....
Los racionales unidos a los irracionales conforman un conjunto mayor llamado Los Reales.
Veamos esto en un esquema:
============
IR contiene a Q
IR contiene a Q*
IR contiene a Z
IR contiene a INo
IR contiene a IN
Q* NO contiene a ninguno de los otros Conjuntos Numéricos!
Y como diagramas de Venn, pero en Brasileiro, ja ja ja !!!!
1)
Los números Reales ( IR ), están formados por la unión de dos conjuntos: Los Racionales ( Q ) y los Irracionales ( Q* ).
es decir,
IR = Q U Q*.
Q: Racionales:
Son aquellos que se pueden escribir como fracción. Incluye a los decimales finitos, los periódicos y los semiperiódicos.
ejemplos:
2,3 (Finito) ;
-3,185 (Otro Finito) ;
0,33333..... (Periódico) ;
-5/8 ;
0,6666.....(Otro periódico) ;
-1/3 ;
2,7891212121212.... (Semiperiódico) ....
Q*: Irracionales:
Son aquellos que NO se pueden escribir como fracción, poseen un desarrollo decimal infinito en el cuál jamás se repite algún tipo de período.
ejemplos:
Al conjunto de los Reales se le conoce también como "El Continuo" ....
Nota:
Toda fracción puede escribirse como decimal, PERO
NO TODO decimal puede escribirse como fracción.
2)
Los números Reales, dijimos, se forman por la unión de los Racionales (Q) y los Irracionales (Q*).
La sola presencia de los Racionales (Q), deja incompleta la Recta Numérica, es decir, si en una recta numérica graficamos Q, que contiene como subconjuntos a IN, INo y Z, la recta estaría llena de hoyos o agujeros .... faltarían infinitos números: Faltarían los Irracionales !!!!
¿ Qué cree Ud., son más los Racionales(Q) o los Irracionales(Q*) ?
3)
Hasta IN, INo, Z y Q, los conjuntos numéricos se llaman ENUMERABLES, porque se pueden hacer corresponder biunívocamente (uno a uno) con los números Naturales (IN) o de contar.
De allí en adelante, es decir, Tanto los Irracionales (Q*), como los Reales ( IR), hablamos de Conjuntos Numéricos NO Enumerables, porque no se pueden hacer corresponder biunívocamente con los Naturales ( IN ).
Esto lo descubrió o al menos lo demostró Cantor.
4)
George Cantor (1845 - 1918): Matemático alemán, de origen ruso, creador de la Teoría Axiomática de Conjuntos, y el primero capaz de expresar formalmente en lenguaje matemático la idea o noción de INFINITO, bajo la forma de un nuevo conjunto numérico, los números Transfinitos.
Las ideas de Cantor acerca del infinito recibieron una crítica generalizada que tal vez agravó su tendencia crónica a la depresión, lo que a su vez le llevó muchas veces a estar internado. Sin embargo su obra se hizo trascendente y fundamental para las matemáticas actuales.
El matemático David Hilbert describió el trabajo de Cantor como "el producto más depurado de genio matemático y uno de los mayores logros de la actividad intelectual pura".
5)
Los números Racionales (Q) son infinitos y también lo son los Reales (R); sin embargo, hay más números Reales que Racionales. Georg Cantor, matemático del siglo XIX, fue el pionero en investigar esta aparente paradoja, remeciendo las bases de la matemática que se conocía al momento: al afirmar que existen distintos tipos de infinitos: algunos mayores que otros.
6)
Infinito: ¡ La PARTE igual al TODO !
Entre los años 1870 y 1880 Cantor y Dedekind iban a operar un cambio REVOLUCIONARIO.
De aquello que se había siempre pensado una imposibilidad: que la parte sea igual al todo, ellos hicieron una propiedad.
Ellos mostraron utilizando la correspondencia biunívoca, que el conjunto de los naturales ( IN: Números de contar ) es tan grande como los pares, por ejemplo, porque se puede hacer una correspondencia biunívoca entre los Naturales y los Pares (o impares).
A este conjunto enumerado (hecho corresponder numéricamente con los naturales) se le llama Infinito Numerable o Enumerable o a veces Infinito Discreto.
De igual forma demostró Cantor que hay tabtos Naturales como Enteros (Z) y Racionales (Q).
¿Pero hay solamente un tipo de Infinito?
¿No se podría, en el infinito, ir más allá de los numerable?
En la imagen, una intervención artística personal a la obra de Max Ernst.
7)
¿Es el numerable el único infinito?
Cantor responde que NO.
La potencia de los números Reales es mayor que el numerable.
En efecto es imposible construir una correspondencia biunívoca entre IN y R.
Es decir, hay infinitamente más puntos en la Recta Numérica que números Naturales (o Cardinales o Enteros, o Racionales).
Tenemos dos Infinitos:
1) El numerable ( IN; INo; Z; Q)
2) el de IR, denominado "El Continuo".
Pero cuidado, de nuevo, por más asombro que le cause: No hay más puntos en todo IR, que en el segmento [0,1].
Pero, ¿Hay otros infinitos más allá del Numerable y del Continuo?
8)
Cantor dice que SÍ, que hay otros infinitos más grandes .... Dice que el conjunto de las partes de un conjunto A, tiene una potencia superior.
El conjunto de todos los subconjunto de IR, posee una INFINITUD MAYOR ....
Podemos partir de IN, luego seguir con Z, Q, Q* y construir sus conjuntos de subconjuntos ....
Hay una infinidad de infinitos.
9)
Dos tipos de Infinitos:
IN: Naturales: Alfa Cero (Infinito Numerable)
INo: Cardinales: Alfa Cero (Infinito Numerable)
Z: Enteros: Alfa Cero (Infinito Numerable)
Q: Racionales: Alfa Cero (Infinito Numerable)
------------------------------------------------------------
Q*: Irracionales: Alfa 1 (Infinito No Numerable)
IR: Reales: Alfa 1 (Infinito No Numerable)
10)
El infinito que a mi me gusta ....
Katsushika Hokusai, uno de los artistas japoneses más conocidos a nivel mundial, realizó cerca de treinta mil obras de arte a lo largo de su carrera. Aunque su estilo dista mucho del arte tradicional japonés, su obra es clave en las historia de la producción artística de este país.
Hokusai nació en 1760, en el seno de una familia de artesanos en la provincia japonesa de Edo. Comenzó a pintar desde que tenía seis años, muy probablemente bajo la tutela de su padre, cuyo trabajo era hacer espejos y decorar los marcos con meticulosas ornamentas. En 1779 publicó sus primeras piezas de ukiyo-e –estampas japonesas que mostraban distintas costumbres– como parte de una serie de impresos sobre teatro Kabuki. Durante su primera etapa creativa su estilo se regía por la tradición japonesa, tanto en técnica como en temática, pero a finales del siglo XVIII adquirió varios grabados calcográficos en cobre hechos en Francia y Holanda, que lo llevaron a explorar con diferentes estilos de Occidente. Esto influyó en los temas que trataba en sus obras, se alejó de los actores Kabuki y los cortesanos para enfocarse en el paisaje y en imágenes cotidianas de la vida en Japón, un cambio fundamental tanto para el artistas como para el género ukiyo-e.
La obra más famosa de Hokusai es Treinta y seis vistas del Monte Fuji, una serie de 36 xilografías realizadas entre 1831 y 1833. En una segunda publicación se añadieron diez xilografías más a la serie en las que el artista japonés retrata al Monte Fuji desde diferentes perspectivas y en distintas condiciones climáticas.
La gran ola de Kanagawa, también conocida como La gran ola, es la pieza más reconocida de la serie y de la carrera de Hokusai. De ésta se realizaron miles de copias, y varias llegaron a manos de coleccionistas europeos. A partir de la década de 1870, La gran ola se volvió muy popular entre artistas y coleccionistas franceses.
Cristalografía
Boris Delaunay y la cristalografía matemática
Published 15/03/2015 Aut.: M. Macho
El matemático Boris Nikolaevich Delaunay (o Delone, 1890-1980) cumpliría hoy 125 años.
Padre del físico Nikolai Borisovich Delone(1926-2008), trabajó en álgebra abstracta y en teoría geométrica de números.
Utilizó resultados de Evgraf Fedorov (1853-1919), Hermann Minkowski (1864-1909),Georgy Feodosevich Voronoi (1868-1908) y otros matemáticos en el desarrollo de la teoría de cristalografía matemática y modelización matemática de cristales.
Inventó en 1934 la hoy llamadatriangulación de Delaunay, que con todos los circuncentros es el grafo dual de un diagrama de Voronoi: es decir, los vértices del diagrama de Voronoi son los centros de los círculos circunscritos de los triángulos de la triangulación de Delaunay; las aristas del diagrama de Voronoi se sitúan sobre las mediatrices de las aristas de la triangulación de Delaunay.
Superposición de un diagrama de Voronoï (en rojo) y de su triangulacón de Delaunay (en negro)
Los conjuntos de Delone en teoría de espacios métricos también llevan su nombre, y se utilizan, por ejemplo, en teoría de códigos o en teoría decuasicristales.
Más información:
- Boris Nikolaevich Delone, The MacTutor History of Mathematics archive, University of St Andrews
- Mathematics Genealogy Project
- Triangulación de Delaunay
Suscribirse a:
Entradas (Atom)