sábado, 31 de octubre de 2015
Educación Subversiva
miércoles, 28 de octubre de 2015
Probabilidad de Sucesos Complementarios - 8avo.

Suma de Probabilidad - Sucesos NO Mutuamente Excluyentes - 8avo.

Diciendo abreviadamente .....
Dados dos eventos A y B, subconjuntos de un espacio muestral E de cierto experimento aleatorio, la probabilidad de que ocurra A o B o ambos está expresada en la siguiente Ley de Probabilidad Total:

Suma de Probabilidades - Sucesos Mutuamente Excluyentes - 8avo. Medio
Para sucesos Mutuamente Excluyentes el cáculo de la probabilidad de que ocurra uno de los dos sucesos es la suma de las probabilidades de ocurrencia de cada uno de los sucesos en cuestión.
Si los sucesos A y B son mutuamente excluyentes, entonces:

Razón de Oro .....
Phi - The Golden Key
The Golden Key - a video by Jonathan Quintin Art
Posted by Jamie Janover on domingo, 25 de octubre de 2015
martes, 27 de octubre de 2015
El último Teorema de Fermat (Por Adrián Paenza)
Pierre de Fermat vivió entre 1601 (o 1607, o 1608. la fecha de su nacimiento es dudosa) y 1665. Nació cerca de Toulouse, Francia, y se recibió de abogado en la Universidad de Orleans. Hablaba varios idiomas: latín, griego, italiano, español y, obviamente, francés. [1] Sin embargo, si bien su palabra y su opinión eran muy buscadas dentro del ámbito del derecho, hizo su aporte más importante a la historia de la humanidad como matemático.
Curiosamente, Fermat no se consideraba a sí mismo como tal. De hecho, hacía sus afirmaciones a través de cartas a sus amigos (Pascal, entre otros) y, en general, tendía a no ofrecer las clásicas demostraciones que los matemáticos consideran (consideramos) imprescindibles para que algún aporte sea juzgado válido. Eso le garantizaba, en algún sentido, la vigencia de su condición de amateur. Fermat no se sentía obligado a hacer lo que tenían que hacer todos los demás: probar lo que decía.Algunas veces lo hacía. Otras (muchas), no.
Esto no pretende quitarle ningún mérito, ya que con el tiempo Fermat se convertiría en el padre de lo que hoy se denomina la teoría de números, que es la que estudia -entre otras cosas- las propiedades de los números enteros. De hecho, él se habrá considerado un amateur, pero sus ideas revolucionaron una parte de la ciencia. Sus cartas con Pascal fueron el origen de la teoría de probabilidades. Y virtualmente transformó todo lo que tocó en matemática.
Pero lo que Fermat nunca soñó (creo) fue que terminaría haciendo -involuntariamente- un aporte inigualable. En 1650 escribió una nota en el margen de un libro que estaba leyendo (Arith- metica, de Diofantino) en la que afirmaba que la ecuación
Lo curioso es que Fermat se murió y nunca llegó a publicar la justificación de lo que decía. Su hijo, muchos años después, hizo pública una copia de lo que su padre había escrito en el margen del libro (el original nunca apareció) y eso iniciaría la verdadera historia. Poco antes de morir, Fermat dejó planteadas varias incógnitas que con el tiempo se fueron comprobando. Con una excepción... una sola excepción: lo que se empezó a conocer con el nombre de “La conjetura de Fermat”. [2]
Los matemáticos más importantes de la historia (Euler, Dirichlet, Gauss, Lamé, Kummer, Sophie Germain..., entre otros) intentaron probarla pero no pudieron. Se resolvían casos particulares, sí, pero no se encontraba la solución general. Ya no eran sólo algunos años, sino que empezaron a pasar siglos y la pregunta seguía vigente: lo que había dicho Fermat ¿era cierto o falso?
Lo más frustrante era que el enunciado del problema resultaba tan sencillo que generaba fastidio no poder resolverlo. Hasta que apareció en escena Andrew Wiles (nacido en Cambridge, Inglaterra, en abril de 1953). Cuando tenía 10 años, un maestro de matemática de la escuela les contó a los alumnos sobre este problema que había enloquecido a los especialistas por más de trescientos años y que se conocía con el nombre de “La conjetura de Fermat”.
Wiles, según su propia confesión, se propuso ser matemático y fantaseó con ser él quien lo resolviera. En 1975 empezó su carrera como investigador, pero fue en 1986 cuando -ya como profesor en Princeton- decidió dedicar entre doce y catorce horas diarias a desentrañar la solución del problema. Sin embargo, no quería comunicar a sus colegas lo que estaba haciendo, porque creía que todos lo entenderían como una pérdida de tiempo. Sólo su mujer, Nada Canaan, sabía lo que hacía en el altillo de su casa. Su rutina diaria lo llevaba a la facultad, donde tenía alumnos y dictaba su curso semestral, y mantenía una vida supuestamente normal.
Wiles comprendía que resolver el problema en sí mismo no serviría para nada útil, en el sentido mercantil de la palabra. Pero, como ocurre con todos los científicos, lo importante no necesariamente es encontrar la solución sino valorar y disfrutar de las herramientas que se desarrollan en el camino de la búsqueda. De eso se trataba (y se trata): de generar más matemática, que sirva (o no) para este caso particular, pero que, en el camino, permita que la ciencia avance en múltiples direcciones.
Después de seis años de virtual aislamiento, Wiles necesitó la ayuda de especialistas en otras áreas. Sus ideas eran tan novedosas que terminó ligando ramas de la matemática que no parecían tener relación hasta ese momento. Finalmente, en 1993, Wiles creyó que tenía “la prueba”. Y se propuso contarla en un ciclo de tres conferencias que daría en Princeton.
La sala se encontraba abarrotada de gente, porque si bien no estaba anunciado el verdadero motivo de la charla, el rumor ya se había filtrado y la comunidad matemática esperaba un anuncio espectacular. Las tres conferencias ocuparon tres días y, para finalizar la última, Wiles escribió en el pizarrón la famosa “Conjetura de Fermat”. Dejó la tiza apoyada en uno de los bordes y dijo: “Creo que voy a parar acá”. El auditorio se puso de pie y aplaudió durante varios minutos. La noticia era/fue tan trascendente que apareció en la tapa de los diarios más importantes del mundo, empezando por el New York Times. Había caído la última pared. La “Conjetura...” dejaba de ser tal. Ahora se había convertido en un Teorema.
Pero no tan rápido. Para que una afirmación científica sea aceptada como verdad necesita la aprobación de los colegas, el monitoreo y el arbitraje independientes. Es decir, matemáticos expertos en el tema se disponen a leer exhaustivamente todo lo que está escrito para dar su consentimiento final. O sea: no alcanza con decir “ya lo terminé” o “ya lo probé” para que la prueba sea considerada válida.
Y ahí empezó otra pequeña odisea. Después de tanto entusiasmo y con el mundo expectante por la publicación, los referís no daban por concluida su tarea. Uno de ellos, Nick Katz, había encontrado algo que no entendía. Lo envió como pregunta al propio Wiles para que se lo aclarara, pero éste se dio cuenta rápidamente de que lo que Katz le estaba diciendo era que la prueba tenía un “agujero” (un error o bien algún razonamiento que no estaba bien justificado).
Era septiembre de 1993 y la mujer de Wiles le dijo: “Ahora, la única cosa que quiero como regalo de cumpleaños es que corrijas el ‘error’. Quiero ‘la prueba correcta’”. El propio Wiles, cuando cuenta la historia, dice que su esposa cumple años el 6 de octubre. Sólo le quedaban entre dos y tres semanas. Pero no, no alcanzó. No hubo humo blanco.
Wiles comenzó a desesperar. Los árbitros no podían mantener más tiempo escondido el error. Al final, terminaron comunicándolo. Durante los siete años en los que Andrew había lidiado solo con el problema nunca había tenido que dar cuenta de sus avances ni de sus retrocesos. Desde las charlas en Princeton cada día era un calvario.
Un año después, con la ayuda de uno de sus estudiantes, Richard Taylor, Wiles se sintió tentado de anunciar que se daba por vencido. Pero la mañana del 19 de septiembre de 1994 tuvo una idea. Le corrió un sudor frío por el cuerpo porque advirtió lo que había pasado: había encontrado la solución. Ahora sí, los referísestuvieron de acuerdo y la prueba fue aceptada como tal. La reina de Inglaterra lo nombró “Sir Andrew Wiles” y su nombre pasó a engrosar la lista de los matemáticos más famosos e importantes de la Historia.
Es muy poco probable que lo que a Fermat no le hubiera entrado en el margen fuera la demostración correcta. En cualquier caso, es irrelevante. La moraleja será siempre que la solución en sí misma es la zanahoria que estimula, el motor del pensamiento... pero nunca es el objetivo último. En el trayecto se abren nuevos caminos y se desarrollan nuevas herramientas, que quizá resulten estériles en la búsqueda de esasolución en particular, pero que son los cimientos de la nueva ciencia.
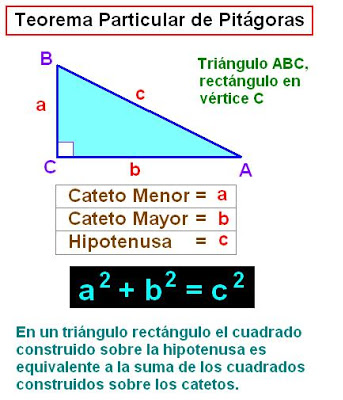
El problema es realmente muy sencillo de entender (véase la ecuación (1)). El teorema de Pitágoras dice que “en un triángulo rectángulo (que tenga un ángulo recto, como en una escuadra.), el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los catetos”.

Figura 1
Notas:
lunes, 26 de octubre de 2015
Francisco Varela
Ohhhhhh nooooooooooo ...... Cara o Sello (Cara o CECA)
Si hay algo que le falta a este mundo cada vez más controvertido es que venga alguien y diga que tirar una moneda al aire no ofrece un 50 por ciento de posibilidades de que salga tanto cara como ceca (suponiendo que la moneda no está “cargada”). Es decir, si hay algo que uno da como seguro en la vida es eso: 50 por ciento para cada lado, cara o ceca. Es algo así como una manera de vivir.
Pero, ahora, necesito decir: ¡no tan rápido! No esté tan seguro de que es así.
No crea que a mí no me impacta escribirlo tanto como a usted leerlo. La noticia me desconcertó a mí también, y si no fuera por la seriedad de los involucrados –los responsables intelectuales– no le habría dado mayor crédito. Pero, como Persi Diaconis es uno de los autores del trabajo, vale la pena prestar atención.
¿Quién es Persi Diaconis?
Persi Diaconis nació en Nueva York, en enero de 1945, en una casa de músicos. Durante muchísimos años fue mago profesional. Sí: mago. Dejó el colegio a los 14 años y se dedicó a recorrer Estados Unidos con Dai Vernon, considerado “el mejor mago de la historia norteamericana”.
Diaconis era tan bueno generando nuevos trucos y aportando nuevas ideas que empezó a ganarse la vida haciendo magia. Pero su pasión, según su propia confesión, era estudiar probabilidades. Por lo tanto, a los 25 años terminó inscribiéndose en el New York City College y se graduó dos años y medio después. Curiosamente, no bien se graduó fue invitado como estudiante de doctorado en Harvard, nada menos, donde se doctoró en 1975. Y allí, en Harvard, es donde ha trabajado la mayor parte del tiempo.
Lo interesante de Diaconis es que dedicó su vida a estudiar cosas que al resto de los humanos nos parecerían marginales. Por ejemplo, lo que lo hizo famoso casi instantáneamente fue que, en un trabajo muy celebrado (*), demostró que si uno mezcla un mazo de cartas sosteniendo la mitad de esas cartas en cada mano y las entrelaza como se hace en los casinos, entonces, alcanza con mezclar siete veces. Todo lo que uno haga después es irrelevante.
Es decir: si al terminar una “mano” de cualquier juego de naipes, uno quiere tener la garantía de que el mazo quedará bien mezclado, alcanza con mezclarlas siete veces.
Algunos autores señalan que con cinco o bien seis veces es suficiente, pero teniendo en cuenta los parámetros (matemáticos) que quiere cubrir Diaconis hacen falta siete veces para considerar que las cartas quedan mezcladas al azar.
Diaconis hizo muchísimos otros aportes en matemática, especialmente en temas que tienen que ver con procesos aleatorios (al azar) y usó sus hallazgos con las cartas para otros problemas que parecían, en principio, no tener relación.
El 28 de julio del 2009, David Adler, autor del libro Snap Judgment (algo así como “juicio instantáneo” o “sin pensar”), que está por aparecer este mes, hace referencia a un nuevo trabajo que involucra a Diaconis, esta vez con otros colaboradores: Susan Holmes y Richard Montgomery.
Los resultados son sorprendentes: cuando uno hace que una máquina especialmente diseñada arroje una moneda al aire, y uno puede controlar la fuerza con la que es disparada hacia arriba, entonces, el resultado es predecible y uno puede anticiparlo, tanto que la máquina puede hacer que el resultado sea siempre cara.
Adler dice también en su artículo que esto es esperable, teniendo en cuenta que si uno puede controlar la fuerza, también puede calcular la cantidad de veces que la moneda girará en el aire y, por lo tanto, modificarla (la fuerza) hasta lograr que salga o bien cara o bien ceca.
Sin embargo, lo que es realmente espectacular es notar que cuando hicieron el mismo experimento con seres humanos, si la moneda estaba en posición de cara antes de tirarla, caía un 51 por ciento de las veces también en posición de cara. Y si empezaba en ceca, sucedía lo mismo. Es decir, ¡la posición inicial determina la mayoría de las veces el resultado final! Y para poder escribir “mayoría”, como acabo de hacer, es porque el resultado es mayor a un 50 por ciento.
El trabajo de Holmes, Montgomery y Diaconis (**) dice en el sumario: “Analizamos el proceso natural al arrojar una moneda con la mano. Comprobamos que una moneda arrojada consistentemente tiende a caer en la misma posición en la que salió. Lo que produce este hecho depende de un único parámetro, que es el ángulo entre la normal (perpendicular) a la moneda y el vector momento angular. Reportamos también las medidas de estos parámetros, basados en fotografías de alta velocidad. En condiciones normales, la chance de que (la moneda caiga) en la misma posición en la que salió es de un 0,51 (o sea, un 51 por ciento de las veces)”.
Puede que a usted este episodio le resulte irrelevante. Sin embargo, créame que atenta contra lo que uno siempre sospechó y ahora parece que no es cierto: tirar una moneda al aire fue siempre una garantía de equidad, igualdad.
Habrá que revisar nuestras viejas ideas y estar atentos. Al menos, cuando alguien quiera tirar una moneda delante suyo para definir algo que la/lo involucra, dígale que usted va a ser quien la arroje y quien elija.
Y si quien la va a arrojar va a ser otra persona, pídale ver cuál va a ser la posición inicial y usted elige. Si no la/lo dejan, entonces elija otro método que garantice igual probabilidad porque, desde ahora, tirar una moneda al aire no es más algo confiable.
(*) “Trailing the Dovetail Shuffle to its Lair”, apareció en el Annals of Applied Probabilities, Volumen 2, Número 2, en 1992 (Págs. 294-313), y tiene a Persi Diaconis y Dave Bayer como coautores.
(**) “Dynamical Bias in the Coin Toss” (“Tendencias Dinámicas al Arrojar una Moneda”), publicado en la revista Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, Volumen 49, Ejemplar 2, abril del año 2007, Págs. 211-235.
Nota: El doctor Eduardo Cattani, mi amigo personal, excelente matemático argentino que trabaja en la Universidad de Massachusetts, en Amherst, especialista en Geometría Teórica, Funciones Hipergeométricas y Teoría de Hodge, fue quien me envió el artículo de Adler. Por lo tanto, el crédito le corresponde todo a él.
Amín Tapia (7mo) y Antonia Fuentes (7mo) - hablando desde el video ....
domingo, 25 de octubre de 2015
Marca de Clase - Desafío 8avo. Medio
EXCEL: Generador de Programa de Lanzamiento de Moneda - 7mo y 8avo Varela
El comando
=ALEATORIO( )
en B8, nos permite generar un número aleatorio (random) entre 0 y 1.
-----------------------------------------------------------------------------------------------------------
Cuando salga menor o igual que 0,5, diremos que salió Cara. Con este comando en C8:
=+SI(B8<=0,5;1;0)
Asigna 1 a CARA, cuando el valor del número aleatorio es menor o igual a 5,
o en su defecto asigna 0.
-----------------------------------------------------------------------------------------------------------
Cuando salga mayor que 0,5, diremos que salió Sello. Con este comando en D8:
=+SI(B8>0,5;1;0)
Asigna 1 a SELLO, cuando el valor del número aleatorio es mayor a 0,5,
o en su defecto asigna 0.
-----------------------------------------------------------------------------------------------------------
Luego se totalizan las veces que sale cara (Acumulamos en G7)
y se divide por 100, porque son 100 los lanzamientos.
Esto nos da la probabilidad de CARA (En H7).
-----------------------------------------------------------------------------------------------------------
De la misma forma se totalizan las veces que sale sello (Acumulamos en G8)
y este resultado se divide por 100, porque 100 son los lanzamientos.
Esto nos da la probabilidad de SELLO (En H8).
-----------------------------------------------------------------------------------------------------------
sábado, 24 de octubre de 2015
Hummmmmm cine matemático

Educación 3.0 acaba de publicar esta lista de 15 películas basadas en las matemáticas con la idea de que ver películas en las que los conceptos matemáticos son de alguna manera los protagonistas puede ayudar a desarrollar un interés y la curiosidad por ellas:
- El número 23, la historia de un hombre que descubre el poder del número 23.
- 21 Black Jack, hackers contra los casinos de Las Vegas.
- La ecuación preferida del profesor, cuyo protagonista, profesor de matemáticas, carece de memoria más allá de los últimos 80 minutos debido a un accidente.
- La verdad oculta (Proof), con una protagonista que estudia matemáticas cuyo padre descubrió antes de morir un importante cálculo relacionado con los números primos.
- El indomable Will Hunting, sobre un joven con un gran talento para las matemáticas pero con enormes problemas personales.
- La Pizarra, sobre dos profesores que recorren Kurdistán iraní en busca de alumnos a los que enseñar a leer y escribir.
- Contact, un primer contacto con seres extraterrestres en el que las matemáticas son imprescindibles para avanzar.
- Una mente maravillosa, sobre el economista y matemático John Forbes Nash.
- La soledad de los números primos, en concreto de los números primos gemelos.
- Los crímenes de Oxford, en la que un profesor y un estudiante tendrán que descifrar la lógica tras unos asesinatos para intentar parar al asesino.
- Pi, fe en el caos, protagonizada por un geek convencido de que las matemáticas pueden explicar la naturaleza aunque esta nos parezca caótica.
- Cube, en la que varias personas se despiertan en una habitación conectada a su vez a otras seis habitaciones muy similares que encierran trampas mortales; las matemáticas serán una herramienta básica para los protagonistas si queiren sobrevivir.
- Donald en el país de las matemáticas, una para los peques.
- La habitación de Fermat, sobre cuatro matemáticos que son encerrados en una habitación que mengua.
- El pequeño Tate, protagonizada por un niño pequeño superdotado para las matemáticas y su madre, que se esforzará en que el niño pueda dar lo mejor de si mismo a pesar de su complicada situación familiar.
miércoles, 21 de octubre de 2015
¿Para qué sirven las matemáticas?
La gran pregunta, el gran dilema, ¿para qué sirven las ciencias matemáticas? Es la ciencia más abstracta, la da soporte al resto de ciencias, pero a la vez es la ciencia más incomprendida, más alejada de la cultura popular. Se suele alegar como motivo, y como leitmotiv, que su utilidad en la vida cotidiana es dudosa.
Pero cuando alguien pregunta "¿para qué sirven las matemáticas?", no se refiere a cómo y en qué se utilizan las ciencias matemáticas, sino más bien "¿por qué tuve que estudiar y aguantar eso toda la vida?". La respuesta es compleja, como la raíz cuadrada de -1.
Hay dos respuestas tipo. Una, la respuesta mayoritaria quizá, defiende que las matemáticas son una estructura lógica que son bellas por sí mismas, que cuestionarse su utilidad es como cuestionar la utilidad del amor o de la poesía. La segunda respuesta va más a las matemáticas como base de un todo, y que sin ellas no aguantarían los puentes, ni tendríamos computadoras, y que sí se utilizan a diario, por ejemplo, en la seguridad bancaria y de internet se utilizan números primos muy grandes para encriptar información... vamos, la respuesta sería "las matemáticas están detrás de todo", como la espalda.
Pero existe una tercera respuesta, una respuesta como mixtura de estas dos y que alega lo siguiente: es verdad que las matemáticas tienen una belleza propia, y no tienen por qué tener una utilidad, es una torre lógica de conocimientos absolutos, incuestionables; pero también es verdad que se utilizan en cualquier ciencia, en cualquier tecnología, y están tras cualquier modelo que intente explicar nuestra realidad; pero sobre todo, las matemáticas gozan de creatividad y de lógica y todo lo permean, las matemáticas doman la intuición humana.
Por ejemplo, si pudiéramos doblar un papel de 1 milímetro de grosor (una hoja de papel A4 estándar) hasta 50 veces, nos daría la distancia que hay entre la Tierra y el Sol. Esto va en contra de lo que nos diría nuestra intuición. Pero si haces las cuentas, compruebas que es verdad.
Las matemáticas son bellas, sí, son aplicables, también, pero sobre todo, hacen que nuestra intuición no nos engañe, y que nuestra razón nos lleve a alguna verdad. Porque aunque parezca que una piedra dure toda la vida, como un diamante, que se regala como algo eterno, pues no. Un diamante no es para toda la vida, pero un teorema... Eso sí que es una verdad para siempre. Una verdad eterna.
Y con este tema musical, este autotune del artista Iván Lagarto sobre la charla TEDx de Río de la Plata de Eduardo Sáenz de Cabezón, comprobamos la belleza, la utilidad, y lo bailables y divertidas que son las ciencias matemáticas.
Edición y realización: Iván Lagarto y Santi GarcíaReparto: Eduardo Sáenz de Cabezón.Agradecimientos: TEDx Río de la Plata (Argentina) y al arte de Iván Lagarto.
Pirámide - 7mo. Antonia Guerrero
martes, 20 de octubre de 2015
domingo, 18 de octubre de 2015
El cuaderno escocés

El cuaderno escocés supone uno de los documentos más románticos, interesantes e importantes de la historia moderna las matemáticas. Y fue escrito durante las animadas reuniones de los intelectuales de su tiempo. ¿Dónde? En un café, por supuesto.
Viajemos a principios del siglo pasado. A lo que era, por entonces, Polonia. Imaginemos un café, ni demasiado opulento ni tampoco muy cutre. En él hay una mesa; y en la mesa se sientan ocho o nueve personas. Dos de ellas discuten acaloradamente. De pronto se callan. Una comienza a hacer anotaciones frenéticas en una servilleta mientras la otra la mira con desdén. De pronto vuelve a estallar la discusión mientras miran los garabatos de la servilleta. Poco a poco, mientras sigue esta guerra personal, un hombre observa desde uno de lo extremos de la mesa y apunta concienzudamente algunas notas sobre un cuaderno. Este no es otro que el mítico cuaderno escocés, uno de los documentos más interesantes y esclarecedores de la historia de las matemáticas modernas.
Escribiendo el cuaderno escocés
Lwów, es la ciudad de la que hablamos, una pequeña urbe que ahora pertenece a Ucrania. Pero a principios del siglo XX los polacos se habían hecho con el lugar, como cientos de años antes. En aquél momento, tras la Primera Guerra Mundial, la sociedad comenzaba a reestructurarse y la universidad seguía su infatigable trabajo en la búsqueda del conocimiento. Llegamos a los años 30 del siglo XX. Las clases universitarias, que se impartían hasta los sábados en la mañana, no daban descanso a los matemáticos. En aquél entonces, un maduro Stefan Banach se reunía con colegas y alumnos en un café para discutir sobre el tema de su vida: las matemáticas. Cuentan que las discusiones iban desde un animado coloquio hasta encarnizados griteríos que dejaban perplejos al resto de clientes del local. Esto no bastó para que los dueños se cansaran de la presencia de la caterva de matemáticos.

Ni mucho menos. El Café Szkocka albergó las reuniones de estos señores durante bastante tiempo. Eso sí; lo que sí molestaba a los dueños era que los teóricos en traje pintarrajearan las mesas con sus fórmulas y cálculos. O tal vez eran los matemáticos los que se molestaban cada vez que se encontraban las mesas de mármol brillando y sin un solo garabato sobre su superficie. En cualquier caso, según dicen, el desesperado manager del Café Szkocka habló un día con la esposa de Banach, el matemático considerado la cabeza del grupo. Probablemente fue ella la que le dio el cuaderno a su marido, quién comenzó a anotarlo todo en un sitio más prolijo. Así, el 17 de julio de 1935 se anotó el primer problema en la libreta: este es el inicio del cuaderno escocés.
La importancia de un cuaderno
A estas alturas puede que os preguntéis por qué el cuaderno escocés se llama así, si en realidad es Polaco (y casi soviético). Muy sencillo, el Szkocka significa Escocés, en polaco, por lo que el cuaderno no es otra cosa que el cuaderno del café "Escocés". Y este nombre ha trascendido en la historia, tal vez de una manera un poco humilde pero no menos importante. De los participantes en la creación del cuaderno se cuentan nombres importantes de la era moderna de las matemáticas: el propio Banach, Antoni Lomicki, Wlodzimierz Stozek, Hugo Steinhaus o Stanislaw Ruziewicz. El cuaderno en sí no es otra cosa
El cuaderno escocés ha sido una gran influencia dentro de la historia actual de las matemáticas
Los autores, incluso, ofrecían premios tan raros como una oca viva, cenas, caviar o bebidas a quienes fueran capaces de resolver los problemas propuestos. Pero que no os engañe esta curiosidad. Como hemos dicho, entre los matemáticos también habían encarnizadas discusiones y rivalidades. Competiciones que solo los intelectuales pueden vivir con tanta pasión. Pero, ¿qué tiene de especial? El cuaderno representa una conceptualización de numerosos problemas, que dieron pie a nuevos problemas y, probablemente a asentar hipótesis nuevas. El cuaderno terminó siendo custodiado por un camarero al cual, al igual que se piden unas cartas, se le solicitaba el cuaderno.
La Segunda Guerra Mundial sin embargo, supuso el fin de las tertulias. El cuaderno se guardó a buen recaudo durante un tiempo. Años después fue Stanislaw Ulam quién tras recibir el legado de Steinhaus (quién lo había recibido de Mazur) dio a conocer la existencia del cuaderno y su contenido. Muchos de sus autores habían muerto víctimas de la barbarie de la guerra. Por esto y por el romanticismo que lo envuelve, el cuaderno escocés no tardó en mitificarse y convertirse en un objeto codiciado. Se hicieron copias e incluso ediciones comentadas por varios autores. A día de hoy todavía hay problemas sin resolver dentro del cuaderno escocés. Un cuaderno que influyó en las mentes matemáticas del siglo pasado; también ha influido en las de este; y probablemente influirá en las que están por venir. ¿Qué menos se puede esperar de un cuaderno con semejante historia?
Variable Aleatoria, Variable Aleatoria Discreta, Función de Probabilidad - 3ro.Medio - Ángel
Hipotenusa
sábado, 17 de octubre de 2015
jueves, 15 de octubre de 2015
miércoles, 14 de octubre de 2015
lunes, 12 de octubre de 2015
Desafío 2do. Medio: Sistemas de Ecuaciones Lineales 2x2
Problema 1:
a) Desarrollar el cuadrado de binomio, lo que da tres términos, uno de los cuales es x al cuadrado que se cancela con elx al cuadrado del lado derecho.
b) Se multiplica cruzado en la segunda ecuación, para eliminar el denominador.
Problema 2:
a) Se multiplica la primera ecuación por el mínimo común múltiplo (m.c.m.) = 3x2=6
b) Se multiplica la segunda ecuación por el mínimo común múltiplo (m.c.m.) = 4x3=12