Fractal de Fibonacci

Hay entes matemáticos que, por alguna misteriosa razón, necesitan tener protagonismo, necesitan sentirse importantes. Para conseguirlo intentan por todos los medios aparecer en cualquier situación, en cualquier lugar. O al menos eso parece.

Uno de ellos, como ya sabemos, es el número 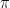, al que podemos encontrar en los lugares más insospechados (como en la probabilidad de escoger dos números primos relativos). Elnúmero  no le va a la zaga, también aparece en lugares donde no se le espera (elmatching problem es un buen ejemplo). Y, sin lugar a dudas, el número áureo, 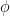, y, en general, la sucesión de Fibonacci poseen la misma característica. La podemos encontrar junto al triángulo de Pascal, en animales y tarjetas o en otras situaciones relacionadas con la naturaleza. Pero, ¿en un fractal? Pues sí amigos, la sucesión cuyo estudio comenzó Leonardo de Pisa, Fibonacci, es otro de esos conceptos matemáticos que nunca dejarán de sorprendernos.

ClaraGrima tampoco dejará de sorprendernos nunca. En lo que se refiere a las matemáticas, nos sorprende gratamente cada dos semanas (más o menos) con Mati y sus Mateaventuras, blog que escribe dentro de Pequeño Libro de Notas. Ahí es donde ella habló hace unos días sobre el fractal de Fibonacci, construcción que paso a contaros con su permiso (gracias por las imágenes Clara).

Partimos de un triángulo rectángulo isósceles (es decir, con sus dos catetos iguales) como el de la figura:

Trazamos la altura desde el ángulo recto, dividiendo así el triángulo inicial en dos triángulos rectángulos iguales. En uno de ellos volvemos a hacer lo mismo, dividirlo en dos más pequeños, y borramos uno de ellos. Estamos en esta situación:

De entre los triángulos que han quedado sin borrar elegimos el de mayor área y lo coloreamos de otro color, verde por ejemplo. Tenemos lo siguiente:

Ahora hacemos lo mismo con este triángulo verde. Trazamos la altura desde el ángulo recto y en una de las dos mitades volvemos a trazar la altura desde el ángulo recto y borramos una de las dos partes creadas. Queda así:

De la figura resultante seleccionamos los triángulos que tengan mayor área y los coloreamos de verde. Ahora queda dos:

Y seguimos igual. En cada uno de esos triángulos verdes trazamos la altura desde el ángulo recto, dividiéndolos así en dos mitades, y ahora en una de las mitades de cada triángulo hacemos lo mismo y borramos otro trocito:

¿Cuántos hay ahora con la mayor área posible? Pues tres, los coloreados de verde:

Repetimos el proceso en esos tres triángulo, y al finalizarlo coloreamos los que tenga mayor área…que resultan ser cinco:

Y si hacemos lo mismo en estos cinco, al final del proceso obtenemos ocho triángulos verdes:

Y una vez más…¿Cuántos triángulos acabarán coloreados de verde ahora? Pues sí, 13:

Y en la próxima habrá…exacto, 21:

Parece clara la regularidad que siguen las diversas cantidades de triángulos que coloreamos de verde, ¿verdad?: 1, 1, 2, 3, 5, 8, 13, 21,…Vamos, los elementos de la sucesión de Fibonacci.

Si eliminamos las líneas sobrantes y coloreamos igual todos los triángulos que nos han quedado obtenemos el siguiente elemento de la sucesión de Fibonacci, 34 en este caso:

Y si añadimos todos los triángulos que habíamos eliminado y coloreamos con el mismo color los que tenga la misma área volvemos a obtener los elementos de la sucesión de Fibonacci (contando los que tiene el mismo color):

No me negaréis que es precioso, ¿verdad? De las construcción más curiosas, interesantes, sorprendentes y bellas (en el sentido matemático) que he visto en los últimos tiempos.

Este fractal de Fibonacci se conoce también como el Racimo de Grossman por su “autor”, George W. Grossman, quien dio una descripción del mismo en Fractal Construction by Orthogonal Projection using the Fibonacci Sequence (pdf) en 1997.